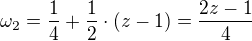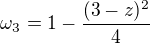Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rovnoměrné rozdělení (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 12. 2018 19:27
Rovnoměrné rozdělení
Dobrý den, prosím o radu pří řešení tohoto příkladu:
X a Y jsou nezávislé náhodné veličiny typu Ro(0,1). Máme vyšetřit náhodnou veličinu Z=2X+Y. A máme některé věci řešit pomocí obrázku.
minimum Z je pro 2*0+0 = 0 .. pokud bude Z<0 tak F(Z)=0
maximum Z je pro 2*1+1=3 ... pokud bude Z>3 tak F(Z)=3
hodnoty 0-3 jsme měli rozdělit do intervalů
0<z<1
1<z<2
2<z<3
(zde už nevím proč)
Dále si máme nakreslit obrázek. Přikládám ..
Bohužel však nevím, jak mám přijít na hodnoty F(Z) v jednotlivých intervalech.
Děkuji!
Offline
- (téma jako vyřešené označil(a) Johana16)
#2 18. 12. 2018 00:05 — Editoval Jj (18. 12. 2018 00:06)
Re: Rovnoměrné rozdělení
↑ Johana16:
Zdravím.
Předpokládám, že teď budete hledat distribuční funkci náhodné veličiny Z, tj. funkci
F(z) = P(Z <= z), kde Z = 2X + Y a
F(z) = 0 pro z < 0, 0 <= F(z) <= 1 pro 0 <= z <= 3, F(z) = 1 pro z > 3.
F(z) lze pro 0 <= z <= 3 spočítat pomocí geometrické pravděpodobnosti:
 = plocha části modrého čtverce na obrázku pod přímkou 2x + y = z (pro každé 'z' z intervalu 0-3), tj. plocha oblasti čtverce, v jejichž bodech je 2x + y <= z,
= plocha části modrého čtverce na obrázku pod přímkou 2x + y = z (pro každé 'z' z intervalu 0-3), tj. plocha oblasti čtverce, v jejichž bodech je 2x + y <= z, = plocha celého modrého čtverce (= 1).
= plocha celého modrého čtverce (= 1).
Z toho je už asi zřejmý účel rozdělení z do intervalů uvedených v dotazu.
Pokud se tedy nemýlím.
Offline
#5 29. 12. 2018 22:42 — Editoval Jj (29. 12. 2018 22:45)
Re: Rovnoměrné rozdělení
Jinak - netuším, čeho se poznámka tady ↑ Johana16: týká.
Pokud se tedy nemýlím.
Offline
#7 02. 01. 2019 11:46
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rovnoměrné rozdělení (TOTO TÉMA JE VYŘEŠENÉ)

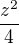 . To by dle výsledků mělo být správně.
. To by dle výsledků mělo být správně.