Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 01. 2019 19:36
#3 24. 01. 2019 19:38
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: ratio of definite integral
@↑ laszky: asked by someone and he told me answer is 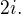 where
where 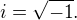
Offline
#4 24. 01. 2019 19:43
#5 25. 01. 2019 22:33 — Editoval laszky (25. 01. 2019 22:36)
Re: ratio of definite integral
Offline
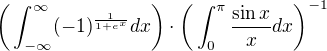
 , for
, for  ?
?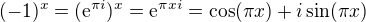 .
.
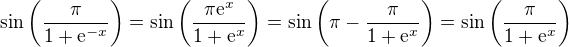
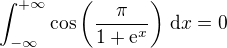 .
.

 :
: