Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 01. 2019 20:41
"kvantová matematika"
Zaujíma ma aký matematický model by dokázal dobre opisovať kvantovú mechaniku. Lebo každodená matematika od sčitania násobenia až po derivácie a integrály je dajme tomu "spojitá" čiže má nejaké to dx infinitideciminial (neviem presne ako sa to píše) tak či by existovalo ničo pri čom by sme mali miesto dx najaké q ktoré je nejaké konkrétne číslo
prakticky všetka matematika je o sčítavaní niečoho
Offline
#2 22. 01. 2019 22:30
Re: "kvantová matematika"
Ale no tak, netřeba v tom hledat takové zázraky. Když budeš hledat možná řešení vlnové rovnice kmitání struny, také dostaneš jen diskrétní frekvence.
Obecně se jedná o tzv. problém vlastních čísel, a v nejjednodušším případě může jít třeba o rovnici 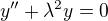
s okrajovými podmínkami ve stylu ,
, 
Snadno zjistíš, že rovnici splňuje funkce
Ale okrajové podmínky se ti podaří splnit jen pro zcela konkrétní hodnoty  takové, že mezi body bude přesně celistvý násobek půlvln.
takové, že mezi body bude přesně celistvý násobek půlvln.
Odtud pochází většina kvantovaných veličin.
V jistém smyslu to lze aplikovat i na spin částic.
Offline
#3 23. 01. 2019 00:21
Re: "kvantová matematika"
↑ MichalAld:
To je dost zavadejici odpoved, protoze neni jasne, proc by mela vlnova rovnice nebo problem vlastnich cisel souviset s kvantovou mechanikou (a ve vetsine konkretnich aplikacich ani nesouvisi).
↑ mateg:
Cislo, na ktere se ptas je Planckova konstanta, ktera udava nejmensi mozne mnozstvi akce (energie). Pomoci Heisenbergova principu neurcitosti pak muzes integraly napr. pres konfiguracni prostor napsat jako konecne sumy.
Matematickych modelu je pro kvantovou mechaniku existuje vice, ty elegantnejsi pouzivaji trochu funkcionalni analyzy v Hilbertovych prostorech.
Offline
#4 23. 01. 2019 11:28
Re: "kvantová matematika"
Tak odpověď je určitě trochu zavádějící, když je trochu zavádějící i ta otázka.
Bati napsal(a):
... ty elegantnejsi pouzivaji trochu funkcionalni analyzy v Hilbertovych prostorech.
Áno, jako třeba hledání vlastních čísel operátorů...
Offline
#5 23. 01. 2019 12:49
Re: "kvantová matematika"
Pozdravujem,
↑ mateg: precitaj si aj toto https://en.m.wikipedia.org/wiki/Mathema … _mechanics
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
