Matematické Fórum

Flaky · 23. 01. 2019 14:58 — Editoval Flaky (23. 01. 2019 15:10)

Zdravím,

dokázal by mě někdo nějak slovně osvětlit definici/význam Minkowského funkce pro nějakou množinu $A$ , tj. $\mu A(x)=inf\{\alpha >0:x\in \alpha A\}$ ?

Dále by mne zajímalo, proč platí (2) a (3) v následujícím důkazu, kde A,B jsou konvexní, neprázdné a disjunktní množiny

//forum.matweb.cz/upload3/img/2019-01/51814_screenshot_20190123_145132.png

byk7 · 13. 04. 2019 17:17

Rozlišme dvě možnosti
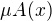- $x\in A$ , pak $\mu A(x)$ říká, jak moc můžeme smrštit, aby ještě stále $x$ leželo v té smrštěné verzi,
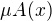- $x\notin A$ , pak $\mu A(x)$ naopak říká, jak minimálně musíme $A$ nafouknout, aby $x$ v té nafouknuté A leželo.
Zejména pokud x leží na hranici množiny A, pak $\mu A(x)=1$ .

Představuju si to jako stejnolehlost s kladným koeficientem vzhledem k nějakému počátku.

Pak by obě vlastnosti měly být jasné.
ad (2)
- x leží na hranici množiny A, pak μA(x)=1,
- x leží uvnitř množiny A, takže můžeme množinu A smrštit tak, abychom x dostali na hranici, tj. μA(x)<1.
ad (3)
- b leží na hranici množiny A, takže μA(b)=1,
- b mimo uzávěr množiny A, pak ale musíme A nafouknout, abychom dostali b na hranici, tj. μA(b)>1.

(Ale nevidím, kde se tam používá ta konvexnost, řekl bych, že nikde.)

Matematické Fórum

#1 23. 01. 2019 14:58 — Editoval Flaky (23. 01. 2019 15:10)

Minkowského funkce

#2 13. 04. 2019 17:17

Re: Minkowského funkce

Zápatí