Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Smíšená parciální derivace funkce více proměnných
#1 31. 01. 2019 23:26
Smíšená parciální derivace funkce více proměnných
Zdravím, mám problém s touto úlohou.
První derivaci jsem udělal podle x. To jsem se pak snažil ještě zderivovat podle y. Ale někde asi dělám chybu, protože při dosazení mi vychází nesmyslný výsledek.
Asi bych měl tu druhou derivaci podle y udělat jinak. Poradíte mi?
Offline
#3 31. 01. 2019 23:41 — Editoval laszky (01. 02. 2019 00:15)
Re: Smíšená parciální derivace funkce více proměnných
↑ -TR-:
Ahoj, prepokladam, ze  a rovnice je
a rovnice je  ?
?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Smíšená parciální derivace funkce více proměnných

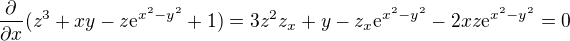
 , a proto
, a proto 

 , a proto
, a proto 

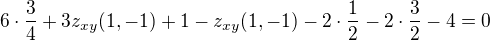 , a proto
, a proto
