Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Diofantická rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 08. 2009 23:48
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Diofantická rovnice
Dobrý večer,
poradíte mi s řešením rovnice
na kladných celých číslech? Pochází ze SAT (Scholastic Aptitude Test), tady je spousta zajímavých příkladů na středoškolské úrovni, bohužel bez řešení...
S podobnými rovnicemi nemám žádné zkušenosti, nevíte o úvodu do problematiky někde na internetu? Klidně AJ
Offline
#2 24. 08. 2009 10:18
#3 24. 08. 2009 17:53
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Diofantická rovnice
↑ Olin:
Děkuju za odkazy a řešení, je mi to jasné. Do další velmi podobné rovnice už jsem se pustil sám, ale po dnu snažení musím uznat porážku, asi mi chybí kreativita. ,
,
tentokrát x, y nezáporná celá čísla. Můj první nápad byl chápat rovnici jako kvadratickou pro y s parametrem x a po eliminaci záporného řešení a úpravě jsem dostal .
.
Následně mě napadlo podle jednoho z odkazovaných materiálů zkoumat dělitelnost  osmi, vychází 1, takže pro nějaké x může odmocnina vyjít přirozená. Musel bych tedy vyzkoušet víc než 1000 hodnot x, je to slepá ulička? Taky mě napadlo využít toho, že grafem té relace je parabola, ale nevím jak, navíc bez počítače bych si toho asi na první pohled nevšimnul...
osmi, vychází 1, takže pro nějaké x může odmocnina vyjít přirozená. Musel bych tedy vyzkoušet víc než 1000 hodnot x, je to slepá ulička? Taky mě napadlo využít toho, že grafem té relace je parabola, ale nevím jak, navíc bez počítače bych si toho asi na první pohled nevšimnul...
Offline
#4 24. 08. 2009 18:29 — Editoval BrozekP (24. 08. 2009 18:30)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Diofantická rovnice


Odmocněním dostaneme  . Z toho ale také plyne
. Z toho ale také plyne  , což dále využijeme.
, což dále využijeme.
Opět odmocníme na  . Máme tedy pouze dvě možnosti pro
. Máme tedy pouze dvě možnosti pro  , z toho už dopočítáme, že řešení je pouze x=13, y=31.
, z toho už dopočítáme, že řešení je pouze x=13, y=31.
Offline
#5 25. 08. 2009 13:57
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Diofantická rovnice
↑ BrozekP:
Díky, řešení rozumím, ale sám bych na něj nepřišel. Můžete mi ještě zkontrolovat jeden o něco jednodušší příklad? ;,x,y kladná celá čísla.
;,x,y kladná celá čísla.
použiju  , potom
, potom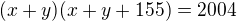 , přitom
, přitom , takže musím nějak tyto čtyři činitele rozdělit mezi dvě závorky na předchozím řádku. Uvědomím si, že ty dvě dvojky musí zůstat "spolu," tj. jako čtyřka, jinak by totiž
, takže musím nějak tyto čtyři činitele rozdělit mezi dvě závorky na předchozím řádku. Uvědomím si, že ty dvě dvojky musí zůstat "spolu," tj. jako čtyřka, jinak by totiž  muselo být kvůli první závorce sudé a kvůli druhé liché, což je spor, čímž dostanu tři možnosti:
muselo být kvůli první závorce sudé a kvůli druhé liché, což je spor, čímž dostanu tři možnosti: , ze kterých vychází jen ta poslední. Rovnici by tedy mělo řešit plných jedenáct uspořádaných dvojic [x,y]:[1,11][2,10]...[11,1].
, ze kterých vychází jen ta poslední. Rovnici by tedy mělo řešit plných jedenáct uspořádaných dvojic [x,y]:[1,11][2,10]...[11,1].
Mám to dobře?
Offline
#7 25. 08. 2009 18:28
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Diofantická rovnice
↑ Olin:
Díky za kontrolu, snad to ještě neni otravný, ale mám tu další. Neumí takové rovnice řešit třeba Wolfram Alpha, nebo podobné nástroje? Mathematicu (dá se to skloňovat?:) bohužel nemám.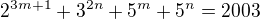
Nejdřív jsem to zkoušel různě logaritmovat, ale nikam to nevedlo. Tak jsem dosadil pár hodnot a zjistil, že ty exponenciály rostou tak rychle, že musí být  . Pak jsem prostě otestoval všech devět dvojic a vyšla jediná, [3,3]. Je to vůbec regulérní řešení? Třeba to jde nějak hezky...
. Pak jsem prostě otestoval všech devět dvojic a vyšla jediná, [3,3]. Je to vůbec regulérní řešení? Třeba to jde nějak hezky...
Offline
#8 25. 08. 2009 19:16 — Editoval lukaszh (25. 08. 2009 19:16)
Re: Diofantická rovnice
↑ FliegenderZirkus:
Na tvoje riešenie sa dá prísť voľbou  . Ja zvyknem pri týchto úlohách voliť rovnosť a zistím, či nejaká dvojica vyhovuje. Predpokladám
. Ja zvyknem pri týchto úlohách voliť rovnosť a zistím, či nejaká dvojica vyhovuje. Predpokladám 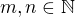 . Čo sa týka riešení
. Čo sa týka riešení  , tak stačí uvážiť
, tak stačí uvážiť
teda ti stačí uvažovať dvojice typu ![kopírovat do textarea $[m,n]$](/mathtex/68/685ca451ac6804ebb521f2c27344d166.gif) , kde
, kde  . Ešte pomôže, že
. Ešte pomôže, že  . Teda
. Teda  pre
pre  . Teda
. Teda  môžeme rovno vypustiť z možností. Osekal som to na
môžeme rovno vypustiť z možností. Osekal som to na ![kopírovat do textarea $[m,n]$](/mathtex/68/685ca451ac6804ebb521f2c27344d166.gif) , kde
, kde 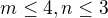 . Vychádza dvanásť možných kombinácii dvojíc. Podobne použi ešte
. Vychádza dvanásť možných kombinácii dvojíc. Podobne použi ešte  a zistíš, že
a zistíš, že  . Počet možných kombinácii sa zníži na 9.
. Počet možných kombinácii sa zníži na 9.
Ale to je v podstate to, k čomu si dospel aj ty :-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#10 25. 08. 2009 20:42
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Diofantická rovnice
Dík za reakce, k tomu odhadu se asi dá dopracovat různě, jen mi to nepřišlo moc "elegantní," ale nic lepšího mě nenapadlo.
Offline
#11 25. 08. 2009 21:44 — Editoval Olin (25. 08. 2009 21:45)
Re: Diofantická rovnice
Tak záleží, v jakých podmínkách to řešíš :-) Třeba na celostátku MO, kde nemáš povolenou ani kalkulačku, by ses možná chtěl vyhnout relativně pracnému zkoušení devíti možností. S kalkulačkou to ale zas není problém… Já se tedy přiznám, že pokud např. vím, že daná rovnice může mít řešení třeba jen od 1 do 1000, tak si napíšu krátký program/skript (zpravidla v Pythonu), který mi všech těch 1000 možností vyzkouší.
Tady mě snad jako finální usnadnění (po tom, co už víme , že obě čísla jsou menší či rovna třem) napadlo jít přes zbytky po dělení pěti.
Řešíme tedy .
.
To už se nám počítá mnohem snadněji - zjistíme, že možné zbytky výrazu 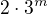 jsou po řadě 1, 3, 4, z čehož už vidíme, že jediný aspirant na řešení je [3; 3]. No a to už musíme vyzkoušet v původní rovnici.
jsou po řadě 1, 3, 4, z čehož už vidíme, že jediný aspirant na řešení je [3; 3]. No a to už musíme vyzkoušet v původní rovnici.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Diofantická rovnice (TOTO TÉMA JE VYŘEŠENÉ)

 musí být celé. Ovšem 2003 je prvočíslo, zlomek tedy bude celý jen pro
musí být celé. Ovšem 2003 je prvočíslo, zlomek tedy bude celý jen pro
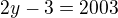 .
. ,
,  . Jelikož 2001 není druhou mocninou žádného celého čísla, není toto řešením.
. Jelikož 2001 není druhou mocninou žádného celého čísla, není toto řešením. ,
, 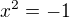 . Myslím, že k tomu není potřeba další komentář :-)
. Myslím, že k tomu není potřeba další komentář :-)
 .
. , coz nelze, nebo
, coz nelze, nebo  , coz ale neni ctverec zadneho celeho cisla. Takze uloha nema reseni. ;-)
, coz ale neni ctverec zadneho celeho cisla. Takze uloha nema reseni. ;-)