Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 03. 2019 18:33 — Editoval Kate X (05. 03. 2019 18:35)
Logaritmická fce
Zdravím,
jak řešit tento příklad ?
log{x}(3) je menší nebo rovno log{x}(11) Mělo by to vyjít x=5.
Z grafu odvodím, že fce musí být rostoucí, tedy x patří do intervalu <0,nekonečno). Nicméně dál s tím nehnu.... Navíc mi připadá, že v daném intervalu tam můžu dosadit cokoli a vzhledem k tomu že funkce bude rostoucí, nerovnice bude platit...
"Když ji miluješ, je pořád co řešit..."
Offline
- (téma jako vyřešené označil(a) Kate X)
#2 05. 03. 2019 19:27 — Editoval Al1 (05. 03. 2019 19:28)
Re: Logaritmická fce
↑ Kate X:
Zdravím,
tvá myšlenka, že nerovnice je splněna, pokud je logar. fce rostoucí, je správná. Ale pro základ logaritmu -zde x- platí: . A co platí pro základ, když má být fce rostoucí? Nemůžeš dosadit cokoli, jak píšeš.
. A co platí pro základ, když má být fce rostoucí? Nemůžeš dosadit cokoli, jak píšeš.
A x=5 není rozhodně jediné řešení. Pokud není v zadání úlohy nějaké omezení.
Offline
#3 05. 03. 2019 19:53
Re: Logaritmická fce
Základ musí být větší než jedna....
K tomu jsem ale došla (aneb když sice myslím, ale prsty píšou do klávesnice něco úplně jiného...). A pořád nevím, jak se z toho dál dostat k výsledku 5. (což máme jako jediný výsledek, ale chyba v tom být může) Ano, více výsledků vidím - celý ten interval, a to asi nebude správně. A nevím co s tím mám udělat... Grafem si už asi nepomůžu, a početně vůbec nevím co s tím.
"Když ji miluješ, je pořád co řešit..."
Offline
#4 05. 03. 2019 20:00
Re: Logaritmická fce
Tak jsem se pokusila použít vzoreček log{a}(b)=log(b)/log(a). Jenže vzhledem k tomu že ten základ je stejný, myslím že se pak jmenovatele vykrátí a x zmizí.... Takže taky vedle. Anebo se do toho zamotávám a dělám nějakou triviální chybu...
"Když ji miluješ, je pořád co řešit..."
Offline
#7 05. 03. 2019 20:28
Re: Logaritmická fce
↑ gadgetka: Děkuji za tip... Mám ale pocit, že to je právě to co jsem už zkoušela... Vychází mi z toho log3 <= log11 ; protože log(x) se vykrátí.... Jenže to x bych právě potřebovala...
"Když ji miluješ, je pořád co řešit..."
Offline
#9 05. 03. 2019 20:40 — Editoval Al1 (05. 03. 2019 20:42)
Re: Logaritmická fce
↑ Kate X:
V postupu navrženém ↑ gadgetka: se nic nepokrátí
To už dořešíš. Za podmínek 
Offline


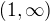 . Jak jsem psal výše, x=5 není jediné řešení. Pokud nemáš v zadání nějaké omezení.
. Jak jsem psal výše, x=5 není jediné řešení. Pokud nemáš v zadání nějaké omezení.