Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
 :
: ![kopírovat do textarea $C^{1}[0,1]->C[0,1] $](/mathtex/ca/ca5915a4ef3ea8f4ab64d767b7878c37.gif) def. tak, že funkci f přiřadí její derivaci, je spojité.
def. tak, že funkci f přiřadí její derivaci, je spojité. tak ze pro vsechna
tak ze pro vsechna ![kopírovat do textarea $f\in C^1[0,1]$](/mathtex/e9/e925690036240b192d6321ff06591600.gif) plati
plati![kopírovat do textarea $\|f' \|_{C[0,1]} \; \leq \; L\, \|f\|_{C^1[0,1]}$](/mathtex/47/477e323ec924e0f8007edec8846c1bd9.gif)
 ?
?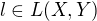 , kde
, kde 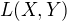 je prostor všech lin. zobrazení mezi X a Y.
je prostor všech lin. zobrazení mezi X a Y.