Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 03. 2019 14:12
Omezenost posloupnosti
Dobrý den, mám zadaný příklad:
a mám vyšetřit omezenost dané posloupnosti.
Nejdřív jsem si určil prvních pár členů.
Posloupnost je tedy klesající a shora omezená jedničkou, která v posupnosti nabývá maxima 
takže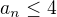


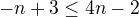
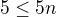

takže je shora omezená jedničkou. A zda-li je zdola omezená zjistím pomocí limity do nekonečna?
Že bych postupoval: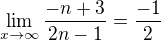
což by znamenalo, že posloupnost je zdola omezená -1/2?
Jednal jsem u celého postupu správně? Děkuji za jakoukoli pomoc
Offline
#2 16. 03. 2019 16:02 — Editoval Ferdish (16. 03. 2019 16:05)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Omezenost posloupnosti
Ako môže byť daná postupnosť zhora obmedzená jedničkou, keď jej prvé tri členy sú väčšie, prinajmenšom rovné 1?
Pri obmedzenosti sa berú do úvahy hodnoty členov postupnosti, nie hodnota jej indexu.
Offline
#3 16. 03. 2019 16:05
Re: Omezenost posloupnosti
↑ Ferdish: takže je tedy omezena 4 shora. A ze zdola je to takhle?
Offline
#4 16. 03. 2019 16:21 — Editoval krakonoš (16. 03. 2019 16:40)
Re: Omezenost posloupnosti
↑ Varagner:
Ahoj.
TY musis dokazat,ze zadana posloupnost an je klesajici napr sledovanim podilu anplus1/an.Pak vyuziji,ze je nezaporna ,tim uz je vlastne zdola omezena,presnou omezenost zdola zjistim limitou.Ale pozor ty jsi spocital pouze limitu exponentu.Dolni omezenost je 2umocneno na vysledek limity.A u limity ma do nekonecna jit n,nikoli x.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#5 16. 03. 2019 16:24
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Omezenost posloupnosti
↑ Varagner:
Pri obmedzení zdola si si vypočítal limitu pre 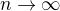 , ale to je len limita exponentu, nie celého predpisu, takže na to pozor...
, ale to je len limita exponentu, nie celého predpisu, takže na to pozor...
Inak, z definície zhora ohraničenej postupnosti podmienku horného ohraničenia spĺňa akékoľvek reálne číslo väčšie alebo rovné 4. Štvorka je zo všetkých týchto čísiel význačná tým, že sa jedná o NAJMENŠIE z horných ohraničení a označuje sa termínom supremum.
Analogicky možno definovať aj najväčšie z dolných ohraničení, ktoré sa zasa nazýva infimum. S týmto sa však študenti v drvivej väčšine zoznamujú až v rámci kurzov matematiky na vysokej škole.
Offline
#6 16. 03. 2019 19:08
Re: Omezenost posloupnosti
↑ krakonoš: Děkuji za odpověď. Takže tedy takhle?
Nejsem si jistý jestli jsem správně pochopil tu omezenost shora. Je tedy omezená 4 a stačí mi to odvození (v uvodnim textu)?
Offline
#7 16. 03. 2019 19:31
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Omezenost posloupnosti
↑ Varagner:
Hypoteticky by to malo stačiť, no lepšie je podľa mňa argumentovať dôkazom, že postupnosť je klesajúca pre rastúce  (čo si odvodil), z čoho vyplýva, že hodnota člena
(čo si odvodil), z čoho vyplýva, že hodnota člena  je horným ohraničením danej postupnosti (dokonca najmenším horným ohraničením).
je horným ohraničením danej postupnosti (dokonca najmenším horným ohraničením).
Offline
#8 16. 03. 2019 19:35
#9 16. 03. 2019 19:57 — Editoval krakonoš (16. 03. 2019 20:17)
Re: Omezenost posloupnosti
↑ Varagner:
Pro dukaz klesajici posloupnosti bych vyuzila klesajici funkci.Funkce 2na xtou je pro kladna x rostouci,funkce 2na minus x tou je klesajici pro kladna x.Podivame-li se na zadani,opravdu to odpovida funkci 2na minus x,pozor,na to v jinych prikladech.Lze tedy porovnat primo argumenty funkce.Pro dukaz klesajici se mi nelibi to rovnitko,je ryze klesajici,dala bych tam ostrou nerovnost.Zkoumame-li nerovnost dvou zlomku,prevedeme je vzdy na stejnou stranu,na spolecny jmenovatel,v tomto pripade je to sice jedno,protoze jmenovatel je pro jakekoli n kladne cislo,ale obecne to vadi.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline