Matematické Fórum

faster29 · 18. 03. 2019 13:26

Mnozstvi 1 molu CO2 expanduje adiabaticky nevratne z teploty 400 K a objemu 35 dm3 proti vnejsimu tlaku 100 kPa do vyrovnani tlaku. Tepelna kapacita CO2 je dana rovnici CVm = 23+27*10-3T [J/Kmol]. Predpokladejte idealni chovano oxidu uhliciteho. Vypocitejte vykonanou W.

Ahoj, počítal jsem to tak, že:
W = -pv(V2-V1)
W = nCvmdT
23*(T2-T1) + 27*10^-3 *(T2^2 - T1^2)/2 = -pv(nRT2/pv -V1)
T2 = 404,15 K

a práce mi vyšla 140,014 J. Můžete mi vysvětlit, kde dělám chybu, když je to expanze a práce má vyjít záporně ? Děkuju

MichalAld · 20. 03. 2019 17:11

A jak vlastně přesně probíhá ta nevratná adiabatická expanze ? Jak je definovaná ta práce, která při ní vznikne ?

KennyMcCormick · 25. 03. 2019 02:24

↑ faster29:
Mně to vyšlo stejně.

Možná má ten plyn tak velký objem/malou teplotu, že se bude místo expanze smršťovat.

↑ MichalAld:
Z toho, co jsem našel, je to jako kdyby se skokem změnil tlak na ten celkový od prvního okamžiku (takže by se to mělo počítat, jak napsal).

MichalAld · 25. 03. 2019 15:21

↑ KennyMcCormick:

Možná v tom mám hokej já, ale já měl vždycky za to, že je buď expanze proti tlaku, nebo nevratná expanze (něco jako expanze do vakua - když otevřeme ventil tlakové lahve, např).

Ale při té nevratné se žádná práce nevykoná, přece. Tam není žádný píst, co by konal práci. A pokud je tam píst, tak je to zase vratné. Pokud se tedy nepohybuje nějak závratně rychle.

Takže mi není úplně jasné, jak se určuje ta práce u nevratné expanze.

rughar · 28. 03. 2019 11:15

↑ MichalAld:

k nevratné expanzi nestačí libovolný tlak. Plyn se při ní musí rozpínat svým vlastním vnitřním tlakem. Cokoliv jiného není vratné. Rozpínání do vakua nebo proti vnějšímu předepsanému tlaku je obojí nevratné. Nemusí ten tlak být nutně nulový.

MichalAld · 28. 03. 2019 15:39

rughar napsal(a):
↑ MichalAld:
k nevratné expanzi nestačí libovolný tlak. Plyn se při ní musí rozpínat svým vlastním vnitřním tlakem. Cokoliv jiného není vratné.

K vratné nebo nevratné ?

Pro mě byl vždycky vratný děj, když byl ve válci píst (obrazně řečeno) a když tam píst nebyl, tak to bylo nevratné. Ale pak zase jako nechápu, jak se určí ta práce.

Znáš nějaký případ, kdy by byl válec s pístem a přitom došlo k nevratnému adiabatickému ději ? Dojde k tomu, když by se píst pohyboval příliš rychle (jen nevím jak rychle by musel - jestli rychleji než je rychlost molekul toho plynu, tuším v řádku km/s, nebo jen rychleji než zvuk, a nebo ještě jinak). Ale pokud se bude pohybovat pomalu - podle mě je to vratné vždycky.

KennyMcCormick · 02. 04. 2019 05:36

k nevratné expanzi nestačí libovolný tlak. Plyn se při ní musí rozpínat svým vlastním vnitřním tlakem. Cokoliv jiného není vratné.
K vratné nebo nevratné ?

Podle mě by první "nevratné" mělo být "vratné".

Pro mě byl vždycky vratný děj, když byl ve válci píst (obrazně řečeno) a když tam píst nebyl, tak to bylo nevratné. Ale pak zase jako nechápu, jak se určí ta práce.

Vratná expanze je, jestli se nepletu, pokud okolní prostředí působí na rozpínající se plyn tlakem, který se pomalu mění od původního tlaku plynu na konečný tlak plynu, zatímco nevratná expanze je ta, kdy je konstantní tlak okolního prostředí od samého počátku.

Takže pro nevratnou expanzi by potom vykonalo okolní prostředí práci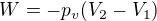
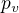$W = -p_v(V_2 - V_1)$ , kde $p_v$ je vnější tlak, 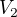$V_2$ konečný objem plynu, 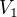$V_1$ počáteční objem plynu. 🙂

(Takže např. při nevratné expanzi do vakua se práce nevykoná.)

rughar · 02. 04. 2019 10:28

↑ MichalAld:

Omlouvám se, mělo tam být vratné. Jde o to, pokud se plyn nerozpíná přesně svým vlastním tlakem, tak dochází k odevzdávání přebytečné práce entropii, udkud již nemůže zpět. Konkrétně, plyn se bude například zahřívat. Kdyby šlo vysloveně o plyn ve vakuu, tak se rozpadne na částice a energie zůstane v jejich kinetické energii.

KennyMcCormick · 05. 04. 2019 05:09

Jde o to, pokud se plyn nerozpíná přesně svým vlastním tlakem, tak dochází k odevzdávání přebytečné práce entropii, udkud již nemůže zpět. Konkrétně, plyn se bude například zahřívat.

Může se stát i něco jiného než zahřívání/ochlazování plynu?

MichalAld · 05. 04. 2019 11:39

↑ KennyMcCormick:↑ KennyMcCormick:
Může se stát také to, že se nestane nic. Jako že teplota zůstane stejná jako předtím. To je také přesně to co se u ideálního plynu stane. Protože vnitřní energie ideálního plynu závisí jen na teplotě - a vnitřní energie se u adiabatického děje nemění.

Pokud neuvažujeme, že by došlo k nějaké chemické reakci, tak jediné, co se může měnit je p, V nebo T. Nic jiné už tam není, ostatní veličiny jsou jen termodynamické potenciály, které lze vypočítat z těch základních.

KennyMcCormick · 07. 04. 2019 08:40

Protože vnitřní energie ideálního plynu závisí jen na teplotě - a vnitřní energie se u adiabatického děje nemění.

Hmm... U adiabatického děje je $Q$ v rovnici
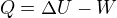$Q = \Delta U - W$ rovno nule, kde $W$ je práce vykonaná okolním prostředím.

Takže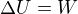
$\Delta U = W$ .

Takže vnitřní energie by měla zůstat konstantní jenom u adiabatických dějů, kdy prostředí nekoná práci (jako je rozpínání do vakua).

MichalAld · 07. 04. 2019 09:30

Je to možné - protože já pořád nevím, co fyzikálně znamená ta "nevratná adiabatická expanze proti tlaku".

Když si představíme klasický válec s pístem, ve kterém je z jedné strany (pístu) ten plyn co nás zajímá a z druhé strany ten konstantní tlak - a druhá strana válce je velmi velmi dlouhá, abychom i při nějakém tom pohybu pístu mohli tlak "zprava" považovat za konstantní, a celé je to zabalené do deky (tepelně izolované), a i píst je zhotoven z izolačního materiálu, tak:

Ještě budeme předpokládat, že má píst nějakou celkem značnou hmotnost, aby se nám pohyboval pomalu. U adiabatických dějů nemusíme nakonec předpokládat (narozdíl od izotermických) že probíhají nekonečně pomalu.

Takže co - stlačený plyn v levé části válce necháme působit na píst - píst se dává do pohybu, získává kinetickou energii, zprava na něj působí konstantní tlak. Až do chvíle, než se tlaky vyrovnají. Plyn v levé části se nám tou adiabatickou expanzí ochlazuje a klesá jeho tlak, plyn vpravo se ohřívá a roste jeho tlak - ale protože je jeho objem velký, můžeme to celkem zanedbat. Nicméně nějakou tu práci obdržel, tu zanedbat nemůžeme.

Dosud je to jasné. Jenže - dosud na tom také není nic nevratného. Práce vykonaná plynem je uložena v kinetické energii toho pístu (nebo si můžeme představit, že pístem zvedáme nějaké závaží a energii jsme si tak uložili někde jinde, to je jedno). Posud bych také rozuměl tomu, co znamená ta "práce vykonaná plynem". Ale dál už mi to úplně jasné není.

Já si tu nevratnou expanzi představuji teda tak, že tam žádný píst není, že jej prostě na začátku odstraníme a počkáme, až se situace ustálí. Nebo do pístu uděláme malou dírku - a zase počkáme až se to ustálí. Teď je otázka co až se ustálí. Zdali jen tlaky, nebo i teploty. Protože když tam ten píst nebude, tak se plyny prostě smíchají a budou mít nakonec i stejnou teplotu.

Ale může to být myšleno i nějak jinak, to já nevím. Pokud je to takto, tak je to ve finále stejné, jako když použijeme náš píst (jak jsem popsal výše) a energii, kterou jsme z něj získali pustíme do topné spirály a ten plyn (v levé části) tím ohřejeme. Pokud jde o ideální plyn, bude mít pak stejnou teplotu jako na začátku (to už jsem zmiňoval v předchozím příspěvku).

Ale pořád mi není jasná ta představa "práce vykonaná plynem". Dokud plyn koná práci, je to děj vratný. Nevratným se stane, když tu práci "zmaříme", když ji přeměníme na teplo.

Asi není úplně správné tvrdit, že "práce se změnila na entropii", protože to jsou dvě rozdílné veličiny (mají rozdílné jednotky), ale pokud by to probíhalo tak, jak jsem to popsal (s tím pístem a topnou spirálou) můžeme říct, že práce se přeměnila na teplo, a to se použilo k ohřátí plynu - čímž se zvýšila i jeho entropie. Pokud tam žádný píst není, tak bych řekl, že ten mezikrok musíme přeskočit a říct přímo to, že se zvýšila entropie plynu.

Víc k tomu už asi nevymyslím. Prostě mi přijde, že má li plyn vykonávat práci, musí tam být ten píst nebo nějaká jeho analogie. Pokud tam píst není, nemůžeme o konání práce mluvit.

Z mého pohledu je úplně jedno, jestli plyn expanduje do úplného vakua, nebo do prostoru kde už nějaký plyn (tlak) je. Já v tom nevidím skoro žádný rozdíl, určitě né žádný takový, který by nás opravňoval tvrdit, že v jednom případě se práce nekoná a ve druhém ano. Navíc jsou to oboje procesy na hony vzdálené termodynamické rovnováze, a klasická termodynamika je stejně nedokáže popsat. Musíme počkat, až se nám to víření ustálí a pak využít toho, že vhodné stavové proměnné nezávisí na způsobu, jakým se systém do stavu dostal.

Takže třeba vnitřní energii či entropii můžeme spočítat tak, že plyn necháme expandovat vratně, a pak jej třeba trochu ohřejeme.

rughar · 07. 04. 2019 20:34 — Editoval rughar (07. 04. 2019 20:37)

Padlo tady tvrzení, že vnitřní energie se při adiabatickém ději neměni. Pozor, to není pravda.

Kdybychom chtěli vyjít trochu z obecnosti, tak platí termodynamický zákon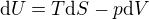

${\rm d}U= T{\rm d}S-p{\rm d}V$

kde

Adiabatický děj: dS = 0
Izochorický děj: dV = 0

U obou dějů však dochází ke změně vnitřní energie. V tom prvním případě je to úměrné změně objemu (rozpínání) a v tom druhém případě změně entropie (výměna tepla). Vnitřní energie se zachovává například při izotermickém ději ideálního plynu. Tam je podle druhé stavové rovnice vnitřní energie přímo úměrná teplotě a nezávislá na tlaku.

Co je potřeba si uvědomit, je význam tepla a teploty. A to nejen na úrovni, že to má jinou jednotku. Teplota se může zachovávat a může se přenášet teplo. Stejně tak je možné přenášet teplo při stálé teplotě. Adiabatický děj je příklad, kdy k žádné tepelné výměně nedochází a přesto se mění teplota. Pokud se plyn rozpíná, koná prácí a v důsledku toho se ochladí. Neochladila ho ale tepelná výměna, nýbrž mechanická práce. Poklesne tím pádem vnitřní energie a v případě ideálního plynu lze za pomocí stavové rovnice i dopočítat, jak se změní teplota.

Dobrá otázka zní, kdy tedy ve skutečnosti nedochází k adiabatickému ději?

Jak jsem psal, adiabatický děj nevyvolává žádnou tepelnou výměnu. Je to čistá mechanická práce. Při ní ale dochází k výrazným změnám teploty. Pokud se potkají dvě prostředí s různou teplotou, zahájí se mezi nimi výměna tepla. Adiabatický děj je tedy realistický v reálném prostředí pouze když proběhne velmi rychle (a nestihne se předat žádné teplo) a nebo když je zkrátka rozpínající se plyn od svého okolí dostatečně izolován.

Pokud tedy máme zajistit, že se plyn rozpínal pod stálým tlakem, už to není možné zajistit pouhým adiabatickým dějem. Při adiabatickém ději plyn koná práci, snižuje se mu vnitřní energie, klesá teplota a klesá i jeho tlak. Abychom udrželi konstatní tlak, musíme ho proto v průběhu děje dostatečně zahřívat. Tím pádem tu máme už tepelnou výměnu. Dokonce nestačí udržovat plyn na stejné teplotě. Musíme ho zahřát ještě více. Protože při izotermickém ději, tlak také klesá s objemem plynu. Ne tak razantně, ale stále klesá. Ve skutečnosti tedy musíme teplotu plynu zvedat, aby měl stále stejný tlak po celou dobu svého rozpínání.

Pro rozpínání také platí rovnice

Adiabatický děj 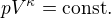$pV^\kappa = {\rm const.}$
Izotermický děj 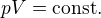$pV = {\rm const.}$

Hodnota kappa záleží na typu plynu, obecně je ale vždy větší než 1 a mělo by být zřejmé, že s narůstajícím objemem u obou dějů klesá tlak a u adiabatického vždy klesá rychleji.

KennyMcCormick · 08. 04. 2019 14:46

↑ MichalAld:

Jenže - dosud na tom také není nic nevratného.

Já bych aplikoval neformální (protože formální definici vratného děje neznám) definici vratného děje jako

reversible process is a process whose direction can be "reversed" by inducing infinitesimal changes to some property of the system via its surroundings

Vratná adiabatická expanze:
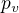Plyn o počátečním tlaku $p_1$ se rozpíná proti tlaku okolí $p_1$ a postupně ztrácí tlak/teplotu. Nakonec jak plyn, tak i okolí skončí na tlaku $p_v$ . Kdybych to udělal pozpátku, budu zvyšovat tlak okolí z 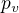$p_v$ zpět na $p_1$ stejným časovým průběhem jako předtím klesal, jenom pozpátku. Plyn se tak postupně vrátí do původního stavu. Děj byl vratný.

Nevratná adiabatická expanze:
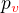Plyn o počátečním tlaku $p_1$ se rozpíná proti tlaku okolí $p_{\color{red}{v}}$ a postupně ztrácí tlak/teplotu. Nakonec jak plyn, tak i okolí skončí na tlaku 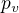$p_v$ . Kdybych to udělal pozpátku, budu držet tlak okolí na tlaku 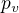$p_v$ a budu čekat, až se plyn začne smršťovat. Ale to se nikdy nestane. Děj byl nevratný.

Otázka je, jak to vypadá, když tam je píst. Možná tak, že píst se bude postupně zpomalovat (protože má určitou rychlost během expanze a na jejím konci má nulovou rychlost (protože plyn dosáhl konečného tlaku, na kterém už zůstane, takže píst se musí přestat pohybovat)), takže se jeho kinetická energie postupně přemění na teplo.

Zdali jen tlaky, nebo i teploty.

Jenom tlaky - to vyrovnání teplot na konci už není součástí adiabatického děje, takže teplota na konci adiabatického děje je teplota před vyrovnáním teplot.

Prostě mi přijde, že má li plyn vykonávat práci, musí tam být ten píst nebo nějaká jeho analogie. Pokud tam píst není, nemůžeme o konání práce mluvit.

To okolní prostředí o určitém tlaku tlačí na ten rozpínající se plyn, takže roli pístu hraje právě to okolní prostředí.

Kdyby byly částice okolního prostředí tak řídké, že by se plyn rozepnul bez interakce s nimi, tak by to bylo totéž jako expanze do vakua a žádná práce by se nevykonala.

Takže třeba vnitřní energii či entropii můžeme spočítat tak, že plyn necháme expandovat vratně, a pak jej třeba trochu ohřejeme.

Jak se takovým způsobem počítá entropie?

↑ rughar:

Při adiabatickém ději plyn koná práci

Pokud se nerozpíná do vakua. 🙂

MichalAld · 08. 04. 2019 16:15

KennyMcCormick napsal(a):
To okolní prostředí o určitém tlaku tlačí na ten rozpínající se plyn, takže roli pístu hraje právě to okolní prostředí.

Jenže tohle není podstatné. Podstatné je, že krom toho, že okolní prostředí vyvíjí tlak, se také chová jako tlumič, že tu získanou energii (práci) dříve či později přemění na teplo.

KennyMcCormick napsal(a):
Kdyby byly částice okolního prostředí tak řídké, že by se plyn rozepnul bez interakce s nimi, tak by to bylo totéž jako expanze do vakua a žádná práce by se nevykonala.

Expanze do vakua se (ve smyslu "tlumení", tedy přeměny práce na teplo) chová úplně stejně jako expanze do oblasti s nižším tlakem.

U mechanického pístu nemusíme nutně uvažovat, že se vykonaná práce promění na teplo. Práci pístu dokážeme přeměnit na jinou energii. Pokud tam píst nebude, tak to nedokážeme - proto je podle mě také dost sporné mluvit o nějaké "práci vykonané při expanzi do plynu či do vakua".

KennyMcCormick napsal(a):
Takže třeba vnitřní energii či entropii můžeme spočítat tak, že plyn necháme expandovat vratně, a pak jej třeba trochu ohřejeme.
Jak se takovým způsobem počítá entropie?

No normálně (dokonce bych řekl, že je to jediný způsob, jak to rozumě spočítat). Adiabatickým procesem (při kterém se entropie nemění) to dostaneme do stavu, kdy to má objem jaký chceme. A pak do toho začneme dodávat teplo (třeba topnou spirálou) - no a teplo, to už je skoro entropie. Skoro, musíme průběžně měřit teplotu (v závislosti na tom, jak dodáváme teplo) a počítat ten integrál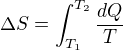

$\Delta S = \int_{T_1}^{T_2} \frac{dQ}{T}$

Ohříváme to tak dlouho, až to dostaneme na požadovanou teplotu. Dodané teplo bychom určili snadno - odpovídá spotřebovanému výkonu. Dodanou entropii musíme spočítat se zohledněním toho, jak se během ohřívání mění teplota.

A protože entropie je stavová veličina, je úplně jedno, jakým způsobem se plyn do cílového stavu dostal - jeho entropie závisí jen na stavu. Takže pokud se plyn do cílového stavu dostal nevratným dějem, bude přírustek jeho entropie stejný, jako jsme to zrovna určili.

MichalAld · 08. 04. 2019 16:28

KennyMcCormick napsal(a):
Nevratná adiabatická expanze:
Plyn o počátečním tlaku $p_1$ se rozpíná proti tlaku okolí $p_{\color{red}{v}}$ a postupně ztrácí tlak/teplotu. Nakonec jak plyn, tak i okolí skončí na tlaku $p_v$ . Kdybych to udělal pozpátku, budu držet tlak okolí na tlaku $p_v$ a budu čekat, až se plyn začne smršťovat. Ale to se nikdy nestane. Děj byl nevratný.

Tohle se hezky napíše .... ale já si teda moc nedokážu představit, jak by něco takového mohlo vypadat v reálu.

Rozpínání plynu není jako přenos tepla přes izolant (že máme na jedné straně izolační vrstvy teplotu T1 a na druhé T2).

Že by jako plyn v nějakém potrubí měl někde tlak p1 a o kus dál p2, to je asi jako trochu utopie. To by fungovalo kdyby tam byla nějaká frita, destička s velmi jemnými póry.

Pokud by tam byla stěna s malým otvorem, bude se tlak takovým dost komplikovaným způsobem spojitě měnit (a v jistých místech bude dokonce menší než p2.

Pokud tam nebude žádná překážka, tak se bude tlak měnit spojitě v dost velké vzdálenosti (díky odporu způsobenému tření o stěny potrubí) a asi když by měl dosáhnout rychlosti zvuku se to ještě bude chovat trochu jinak.

Pokud budeme uvažovat ten případ z fritou (jemně porézní přepážkou), pak to asi smysl dává. Většina práce se zmaří na té fritě (z p1 na p2), a to co zbude nám pak může ve výstupním potrubí pohánět píst tlakem p2. To by pak dávalo smysl.

KennyMcCormick · 09. 04. 2019 15:03

↑ MichalAld:

Expanze do vakua se (ve smyslu "tlumení", tedy přeměny práce na teplo) chová úplně stejně jako expanze do oblasti s nižším tlakem.

U mechanického pístu nemusíme nutně uvažovat, že se vykonaná práce promění na teplo. Práci pístu dokážeme přeměnit na jinou energii. Pokud tam píst nebude, tak to nedokážeme - proto je podle mě také dost sporné mluvit o nějaké "práci vykonané při expanzi do plynu či do vakua".

Z hlediska vykonané práce by to mělo být jiné, protože při expanzi do vakua rozpínající se plyn netlačí silou proti ničemu, takže je jasné, že nekoná práci.

Při expanzi do okolního prostředí tlačí plyn částečně proti ničemu (tam, kde se molekuly plynu nesrazí s molekulami prostředí) a částečně proti okolnímu prostředí, takže to vypadá, jako kdyby práce vykonaná plynem měla být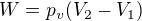
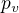$W=p_v(V_2-V_1)$ , kde $p_v$ je vnější tlak, 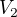$V_2$ konečný objem plynu a 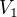$V_1$ počáteční objem plynu.

U mechanického pístu nemusíme nutně uvažovat, že se vykonaná práce promění na teplo. Práci pístu dokážeme přeměnit na jinou energii.

No jo, to je taky pravda. Takže otázka: Proč je takový děj nevratný? Podle mě je nevratný proto, že takový děj nemůže proběhnout pozpátku podle té neformální definice. Cesta tam se odehraje tak, že píst bude uhýbat plynu dostatečně rychle, aby tlačil pouze stálým tlakem 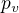$p_v$ (kdyby uhýbal pomaleji, tak tlak pístu bude vyšší než 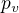$p_v$ a bude postupně klesat na hodnotu 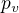$p_v$ ). Cesta zpátky nemůže proběhnout "nekonečně malými" změnami v okolním prostředí - kdyby se totiž píst začal pohybovat nazpět, tlak, který musí vyvíjet, by se okamžitě začal zvyšovat, protože mu v cestě stojí plyn. Takže píst, který bude tlačit pouze tlakem 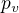$p_v$ , se nemůže vrátit a děj je nevratný.

Takže podle mě není přeměna práce na teplo nezbytnou podmínkou nevratnosti děje.

No normálně (dokonce bych řekl, že je to jediný způsob, jak to rozumě spočítat). Adiabatickým procesem (při kterém se entropie nemění) to dostaneme do stavu, kdy to má objem jaký chceme. A pak do toho začneme dodávat teplo (třeba topnou spirálou) - no a teplo, to už je skoro entropie. Skoro, musíme průběžně měřit teplotu (v závislosti na tom, jak dodáváme teplo) a počítat ten integrál

$\Delta S = \int_{T_1}^{T_2} \frac{dQ}{T}$

Ohříváme to tak dlouho, až to dostaneme na požadovanou teplotu. Dodané teplo bychom určili snadno - odpovídá spotřebovanému výkonu. Dodanou entropii musíme spočítat se zohledněním toho, jak se během ohřívání mění teplota.

Aha, takže z definice přírůstek entropie. To dává smysl.

↑ MichalAld:

Rozpínání plynu není jako přenos tepla přes izolant (že máme na jedné straně izolační vrstvy teplotu T1 a na druhé T2).

Že by jako plyn v nějakém potrubí měl někde tlak p1 a o kus dál p2, to je asi jako trochu utopie. To by fungovalo kdyby tam byla nějaká frita, destička s velmi jemnými póry.

Teď vidím, že vlastně původní dotaz je rozpínaní do okolního vnějšího tlaku a není tam napsané, že okolní prostředí je plyn - takže je otázka, jestli plyn v roli okolního prostředí vůbec může fungovat tak, jak jsem si myslel (ale podle mě je to tak myšlené, protože "vnější tlak" je 100 kPa). Napadá mě buď

1. rozpínání do atmosféry tak rychlé, že si můžeme představit, že se tlak okolní atmosféry nemění, nebo

2. rozpínání, kdy část rozpínajícího se plynu vyplní mezery mezi molekulami vzduchu a druhá část rozpínajícího se plynu do nich narazí - protože nejsme ve stavu termodynamické rovnováhy, tak amosféra může mít jiný tlak než rozpínající se plyn, nebo

3. rozpínání, kdy je veškerá atmosféra tlačena z cesty rozpínajícím se plynem, ale je dost řídká na to, abychom zanedbali, že molekuly atmosféry tlačené z cesty budou narážet na molekuly atmosféry za nimi, odrážet se zpátky proti expandujícímu plynu a tím zvyšovat tlak okolí

Teď se ještě nabízí otázka, jestli tuhle aproximaci můžeme použít. Možná ano - dostatečně řídký (a možná i hustý, nevím) plyn okolního prostředí nebude tlačit na rozpínající se plyn dostatečně silně, takže je za určitých okolností asi lepší to modelovat jako expanzi proti stálému vnějšímu tlaku než jako expanzi proti stejnému tlaku, jako má expandující plyn. (Nebo se ten tlak možná bude měnit, ale způsobem, který plyn zanechá v takovém konečném stavu, který bude podobný tomu, jako kdyby se rozpínal proti stálému tlaku.)

Ale pokud expanze proti stálému vnějšímu tlaku nemůže být (ani přibližně) proti prostředí složenému z plynu (což nevím), tak si tam představíme tu pórézní přepážku.

Matematické Fórum

#1 18. 03. 2019 13:26

adiabatická nevratná expanze

#2 20. 03. 2019 17:11

Re: adiabatická nevratná expanze

#3 25. 03. 2019 02:24

Re: adiabatická nevratná expanze

#4 25. 03. 2019 15:21

Re: adiabatická nevratná expanze

#5 28. 03. 2019 11:15

Re: adiabatická nevratná expanze

#6 28. 03. 2019 15:39

Re: adiabatická nevratná expanze

rughar napsal(a):

#7 02. 04. 2019 05:36

Re: adiabatická nevratná expanze

#8 02. 04. 2019 10:28

Re: adiabatická nevratná expanze

#9 05. 04. 2019 05:09

Re: adiabatická nevratná expanze

#10 05. 04. 2019 11:39

Re: adiabatická nevratná expanze

#11 07. 04. 2019 08:40

Re: adiabatická nevratná expanze

#12 07. 04. 2019 09:30

Re: adiabatická nevratná expanze

#13 07. 04. 2019 20:34 — Editoval rughar (07. 04. 2019 20:37)

Re: adiabatická nevratná expanze

#14 08. 04. 2019 14:46

Re: adiabatická nevratná expanze

#15 08. 04. 2019 16:15

Re: adiabatická nevratná expanze

KennyMcCormick napsal(a):

KennyMcCormick napsal(a):

KennyMcCormick napsal(a):

#16 08. 04. 2019 16:28

Re: adiabatická nevratná expanze

KennyMcCormick napsal(a):

#17 09. 04. 2019 15:03

Re: adiabatická nevratná expanze

Zápatí