Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 03. 2019 22:46
- frankykubo

- Zelenáč
- Příspěvky: 5
- Škola: TUKE
- Pozice: Student
- Reputace: 0
Úloha so syrom
Dobrý deň, mám tu jednu úlohu s ktorou si neviem rady a tak vás prosím o pomoc.
Máme kocku syra s rozmermi 100x100x100 mm. V syre su diery v tvare perfektnej gule, ktoré sa neprekrývajú a sú celým objemom v syre. Cieľom je vypočítať hrúbku každého plátku tak, aby ich hmotnosť bola rovnaká.
Vzorec, ktorý mi má pomocť: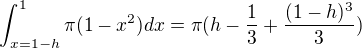
Potrebujem to riešiť všeobecne, pretože z toho musím urobiť algoritmus pre počítač.
Príklad:
Máme M a S, kde M (0 ≤ M ≤ 10 000) určuje počet dier v syre a S (1 ≤ S ≤ 100) je počet plátkov, na ktoré je potrebné syr nakrájať. Ku každej diere máme 4 údaje, a to R, X, Y a Z, pričom R je polomer. X, Y, Z sú súradnice stredu gule. Každý rez je kolmý podľa osi Z. Blok syra okupuje body (X, Y, Z), kde (0 ≤ X, Y, Z ≤ 100 000), okrem bodov, ktoré sú súčasťou diery.
Úlohou je vypísať S hrúbok v milimetroch, začínajúc od konca syra, kde Z = 0. Výsledky môžu mať odchýlku 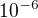 .
.
Offline
#2 19. 03. 2019 18:42 — Editoval Aleš13 (19. 03. 2019 18:44)
Re: Úloha so syrom
Ten vzorec je na vypocet objemu kulove vrstvy, najdi si ho na netu, byva to tam i s obrazky.
Jinak je to cista programatorina. Proste budes pocitat jeden platek za druhym. Vezmes nejaky odhad tloustky, treba M/S, odectes od nej hmotnost der nebo jejich casti (ten vzorec). A vysledek v iteraci upravis podle toho, jestli to byla vice ci mene nez 1/S hmotnosti cele kostky. Ta uprava tloustky budiz treba M/S/4, pozdeji ji budes zmensovat (puleni intervalu staci).
Pak to 1000000krat pustis s nahodnymi daty a kdyz se nekde nezakousne ta iterace, mas hotovo :-)
Offline
#4 19. 03. 2019 21:29 — Editoval rughar (19. 03. 2019 21:31)
Re: Úloha so syrom
↑ Aleš13:
Pokud ma puleni intervalu fungovat, je potreba, aby kazdy platek mel na zacatku tloustku odpovidajici celemu syru, ktery zustal po odkrajeni predeslych casti. Stacila by teda polovina pro kazdy platek, ktery neni posledni. S mensi hodnotou to nebude fungovat.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#5 20. 03. 2019 21:32
- frankykubo

- Zelenáč
- Příspěvky: 5
- Škola: TUKE
- Pozice: Student
- Reputace: 0
Re: Úloha so syrom
Ďakujem za odpovede, skusím to a prípadne sa vám ozvem. :-)
Offline
#6 21. 03. 2019 10:40
Re: Úloha so syrom
Kdyby slo o to delat to s vysokou presnosti (nebo rychle), je lepsi pouzit metodu se superkonvergenci. U puleni intervalu pocet desetinnych mist presnosti roste s poctem iteraci. U superkonvergentnich metod se pocet mist presnosti zdvojnasobi s kazdou iteraci. Na zacatku si tedy tipneme tlousku a spocitame jeho objem 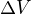 . Pro dalsi iteraci upravime tlousku o hodnotu:
. Pro dalsi iteraci upravime tlousku o hodnotu: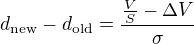
 = plocha platku v rovine rezu
= plocha platku v rovine rezu = objem celeho syru
= objem celeho syru
Dalsi vyhoda, ze se nastrel tipnute tloustky kazdeho platku u tehle motodz nemusi byt veliky, staci kdyz je "blizko". Nabizi se teda na prvni pouzit tloustku hrana_krychle/S a kazdy dalsi zacit s takovou tloustkou, jako vysel predchozi.
Puleni intervalu bude potreobovat radove 30 kroku, tahle metoda radove 3.
1 + 1 = 1 + 1
... a nebo taky ne
Offline