Matematické Fórum

Mr.Luc · 29. 03. 2019 11:22

Ahoj, potřeboval bych poradit s následujícím problémem.
V rámci měření jsme měli stanovit hustotu neznámého tělesa. Byla to krychle, tedy jsme změřili 5x hranu krychle + zvážili těleso.
Jde mi o to, jaký je teď správný postup při stanovení chyby objemu. Protože se jedná o opakované měření, musím počítat statistickou chybu a teď právě nevím, jestli si mám určit průměrnou hodnotu a statistickou chybu pro délku strany a, dostanu tak výsledek

$\bar{a}=a\pm \Delta a$
a z této hodnoty pak teprve určit objem + chybu objemu a následně vypočítat chybu hustoty

nebo z každé hodnoty $a_i$ určit příslušný $V_i$ a z těchto hodnot určit statistickou chybu $V_i$ , nevím ale pak, jak mám vypočítat celkovou chybu objemu, měla by tam být ještě chyba metody. Stačil by mi i jako návod nějaký podobný řešený příklad, tj. takový, kde jsou opakovaná měření a z naměřené veličiny se určí jiná veličina.

MichalAld · 29. 03. 2019 18:22

1) Tohle by mělo spíš vypadat tako, né ?

$a=\bar{a}\pm \Delta a$

2) Jestli nejprve z každé naměřené délky počítat objem a na objemy aplikovat statistiku, nebo naopak, to je celkem jedno. V tom druhém případě ovšem musíš vědět, jak spočítat tu chybu.

A já nevím, jak pokročilou matematiku ovládáš.

Obecně platí, že pokud na změřenou hodnotu aplikujeme nějaku funkci, tedy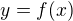

$y=f(x)$

tak pro malou odchylku (zhruba) platí

$\Delta y=f'(x) \Delta x$

Nevím, jestli už umíš derivovat, pokud né, tak ono to v tvém případě půjde i bez toho.
Vzhledem k tomu, že chyba měření bývá malá, můžeme takovýto přístup použít. Kdyby byla chyba měření nějakých 50%, asi už bychom to takto dělat nemohli.

Ty máš funkci $y=f(x)=x^3$ , její derivace je $y'=f'(x)=3x^2$

Takže $\Delta y=3x^2\Delta x$ , ve tvých proměnných to bude $\Delta V=3a^2\Delta a$

Pokud jde o relativní chybu, ta je

$\frac{\Delta V}{V}=\frac{3a^2\Delta a}{a^3}=3\frac{\Delta a}{a}$

To je celkem jednoduchý výsledek, a platí i pro jiné mocniny, pokud je tedy závislost mezi dvěma veličinami určena vztahem $y=x^n$ , tak se relativní chyba zvětší n-krát.

Ještě jsem zmínil, že to jde i bez derivování. Je to asi takto:

$(x+\Delta x)^3 = x^3 + 3x^2 \Delta x + 3x (\Delta x)^2 + (\Delta x)^3$

Pokud je to 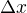$\Delta x$ malé (ve srovnáním s x) tak můžeme ty dva poslední členy zanedbat, a dostáváme náš původní vztah
$(x+\Delta x)^3 = x^3 + 3x^2 \Delta x$

Mr.Luc · 29. 03. 2019 18:49 — Editoval Mr.Luc (29. 03. 2019 18:50)

↑ MichalAld:
Díky moc za odpověď. Matika problém není, ani ta pokročilejší, jen se zatím moc neorientuju v těch chybách:)

Chápu dobře, že uvedený postup je v případě, že si nejprve určím statistickou chybu strany $a$ (takto bych to chápal)?
Jak by to bylo, pokud mám spočítáno, že

$V=1,04\pm 0,01$

tj. spočítal jsem si statistickou chybu až s objemem, ale teď nevím, jak zjistit tu finální chybu, pořád se v tom nějak motám:) , tak jestli nebude lepší to předělat přes tu stranu

MichalAld · 30. 03. 2019 10:33

1) To je jedno, jestli se to dělá přes stranu nebo až přes objem.

Když budeš mít stranu 1+0.01 = 1.01, tak objem bude 1.01 * 1.01 * 1.01 = 1,030301 což je dost přesně 1.03

2) Co je to vlastně ta tvoje "finální chyba" ? Je jen chyba (nejistota) stanovení délky a chyba (nejistota) stanovení objemu. Netuším co je nějaká "finální chyba".

3) A když jsme u toho - žádným vyhodnocením naměřených dat nemůžeš zjistit skutečnou chybu měření, to co děláš je pouze opakovatelnost měření (nebo také náhodná chyba při měření). Pokud bys chtěl určit skutečnou chybu měření, musel by jsi znát správnou hodnotu (velikosti té krychle kterou měříš).

Mr.Luc · 30. 03. 2019 12:53 — Editoval Mr.Luc (30. 03. 2019 13:09)

↑ MichalAld:
Já jsem tam měl právě jen tu statistickou chybu stanovenou pro objem, ale cvičící psala, že bych tam měl ještě pro objem přidat, cituji:
"Co se týče té hustoty, tam byste měl ještě pro objem přidat chybu měření a získat tak výslednou chybu, se kterou pak počítáte dále při výpočtu hustoty".
Právě taky moc nechápu, co tím přesně myslí, ale proberu to pak osobně, to není problém, jen jsem se to snažil před tím vyřešit i sám:)

Nemůže tím myslet toto:

celková chyba= $\sqrt{s^{2}_{\bar{V}}+(\frac{dV}{da}\Delta a)^{2}}$
?

KennyMcCormick · 03. 04. 2019 05:14

Původně jsem ti chtěl napsat tohle:

Autor skryl část textu. Zobrazit/skrýt!

Ale když čtu

Co se týče té hustoty, tam byste měl ještě pro objem přidat chybu měření a získat tak výslednou chybu, se kterou pak počítáte dále při výpočtu hustoty

tak asi chce, abys:

1. Určil celkovou chybu objemu (tak, jak píšu ve skrytém textu, že máš určit celkovou chybu hustoty, ale místo hustoty objem)

2. Určil celkovou chybu hmotnosti.

3. Použil tehle vzorec: https://en.wikipedia.org/wiki/Propagati … lification k výpočtu celkové chyby hustoty z celkové chyby objemu a celkové chyby hmotnosti.

Mr.Luc · 04. 04. 2019 10:33

↑ KennyMcCormick:
Díky moc. Takže jestli to dobře chápu, pro každou vypočtenou hodnotu objemu (5 měření) spočítám chybu měření
$\beta _i=\frac{dV}{da}\Delta a$

A chybu měření pak získám jako průměr těchto hodnot.

Pak vypočtu sttatistickou chybu (to je ok) a celkovou chybu měření objemu dle uvedeného vzorce, to mi dává smysl, díky moc.

KennyMcCormick

Takže jestli to dobře chápu, pro každou vypočtenou hodnotu objemu (5 měření) spočítám chybu měření
$\beta _i=\frac{dV}{da}\Delta a$

Ano. Možná je lepší to napsat jako
$\beta _i=\frac{\partial V}{\partial a}\Delta a_i$ , protože pro funkci jedné proměnné se parciální derivace rovná obyčejné derivaci, ale neplatí to obecně. $\Delta a_i$ místo $\Delta a$ proto, že chyba strany je v tomhle případě pro každé měření stejná, ale neplatí to obecně pro všechny proměnné.

a celkovou chybu měření objemu dle uvedeného vzorce

Ano, a zaokrouhlíš ji na 2 platné číslice.

Mr.Luc · 06. 04. 2019 07:01

↑ KennyMcCormick:Tak super. Díky moc.

Matematické Fórum

#1 29. 03. 2019 11:22

Správný postup při zpracování výsledků měření

#2 29. 03. 2019 18:22

Re: Správný postup při zpracování výsledků měření

#3 29. 03. 2019 18:49 — Editoval Mr.Luc (29. 03. 2019 18:50)

Re: Správný postup při zpracování výsledků měření

#4 30. 03. 2019 10:33

Re: Správný postup při zpracování výsledků měření

#5 30. 03. 2019 12:53 — Editoval Mr.Luc (30. 03. 2019 13:09)

Re: Správný postup při zpracování výsledků měření

#6 03. 04. 2019 05:14

Re: Správný postup při zpracování výsledků měření

#7 04. 04. 2019 10:33

Re: Správný postup při zpracování výsledků měření

#8 06. 04. 2019 04:59 — Editoval KennyMcCormick (06. 04. 2019 05:06)

Re: Správný postup při zpracování výsledků měření

#9 06. 04. 2019 07:01

Re: Správný postup při zpracování výsledků měření

Zápatí