Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spojitost zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
#1 31. 03. 2019 17:42 — Editoval Flaky (31. 03. 2019 17:44)
Spojitost zobrazení
Dobrý den,
chtěl bych se zeptat, kdybych chtěl ukázat, že zobrazení ![kopírovat do textarea $T:C^{1}[0,1] ->C[0,1]$](/mathtex/e2/e2f7312acdfa47120a2203fdef2cf6a8.gif) def. jako T(f)=derivace f není spojité v nule pomocí definice spojitosti přes okolí, tj bych chtěl najít nějakou funkci z okolí
def. jako T(f)=derivace f není spojité v nule pomocí definice spojitosti přes okolí, tj bych chtěl najít nějakou funkci z okolí  , že
, že 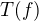 neleží v okolí funkce derivace f, kde okolím funkce
neleží v okolí funkce derivace f, kde okolím funkce  myslím okolí
myslím okolí 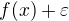 a
a 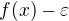 . Jak bych takovou konkrétní funkci mohl najít?
. Jak bych takovou konkrétní funkci mohl najít?
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
- (téma jako vyřešené označil(a) Flaky)
#6 31. 03. 2019 22:35 — Editoval jardofpr (01. 04. 2019 00:51)
Re: Spojitost zobrazení
Flaky napsal(a):
Bohužel, žádná norma mi zadána nebyla. Právě proto jsem chtěl využít definice spojitosti.
no nepôjde to podľa mňa bez normy (alebo predstave o topológii priestorov čo hádam nie je hľadisko tvojho cvičenia)
v pôvodnom príspevku píšeš vágne o okolí .. t.j. buď máš aspoň normu alebo nejak definované otvorené množiny
nemáte niečo také že ak sa nepovie inak beriete nejakú konkrétnu normu?
my sme mali kedysi ak si dobre spomínam napr. na ![kopírovat do textarea $C^k[a,b]$](/mathtex/fc/fc06b510d77beed2cea588f264b06ba4.gif) priestore
priestore ![kopírovat do textarea $||f ||_{C^k} = \sum_{i=0}^k\sup_{x\in [a,b]}|f^{(i)}(x)|$](/mathtex/bc/bc050fc58662db5cf315d209e833022a.gif)
a tú sme brali automaticky ak nebolo uvedené inak
to by znamenalo spojité zobrazenie v tomto prípade, ale nemusí to byť tak ak pracuješ s inými normami
Offline
#7 01. 04. 2019 08:03
Re: Spojitost zobrazení
↑ jardofpr: No, spojitost jako takovou na top. vektorových prostorech máme definovanou, právě proto bych toho chtěl využít.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#8 01. 04. 2019 11:26
Re: Spojitost zobrazení
↑ Flaky: to je síce fajn že to máte definované,
ale keby si chcel toto overovať z definície spojitosti na TP tak mi to príde že musíš tiež vedieť
s akým systémom otvorených množín pracuješ na daných priestoroch
čo mimochodom tuším že keď tak nebude žiadna sranda
určite si napísal celé zadanie?
Offline
#9 01. 04. 2019 16:37
Re: Spojitost zobrazení
Presne tak.. Aby slo mluvit o spojitosti T, je treba znat topologii na X a Y. Navic, co se tyce mnozin C a C1, myslim ze jsem nikdy nevidel "rozumnou" topologii, ktera by nebyla zadana nejakou normou a v tom pripade se s temi okolimi da pracovat v podstate stejne jako v Euklidovskem prostoru. O trochu zajimavejsi to je teprve s  .
.
Offline
#10 01. 04. 2019 19:34
Re: Spojitost zobrazení
↑ jardofpr:
Ano, určitě jsem napsal celé zadání.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#14 16. 04. 2019 00:56
Re: Spojitost zobrazení
↑ vlado_bb:
Co je myšleno tím, že je funkce blízko nuly?
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#16 16. 04. 2019 06:59 — Editoval Flaky (16. 04. 2019 07:03)
Re: Spojitost zobrazení
↑ vlado_bb:
Tj toto ?
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#19 16. 04. 2019 09:57
Re: Spojitost zobrazení
↑ Flaky: Ano, presne tak. Teda - cielom je ukazat, ze pre (napriklad) 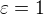 nie je mozne najst vhodne
nie je mozne najst vhodne  . K tomu staci ukazat ze existuje funkcia lubovolne blizka nule s pomerne velkou derivaciou ... ale to sa uz opakujem.
. K tomu staci ukazat ze existuje funkcia lubovolne blizka nule s pomerne velkou derivaciou ... ale to sa uz opakujem.
Offline
#20 16. 04. 2019 13:09
Re: Spojitost zobrazení
↑ vlado_bb:
Hm, kdybych si vzal ln(x), pak na <0,1> je supremum ln(1)<1, , ale 1/x na <0,1> má sup neomezené..
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#22 16. 04. 2019 13:46
Re: Spojitost zobrazení
Panove, prijde mi, ze to tu hrozne motate. Tohle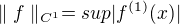
neni ani norma (kvuli konstatnim funkcim). Kdyz uz tak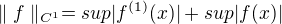 ,
,
ale v tom pripade plyne okamzite z definic ze operator derivace je spojity z C1 do C. Pokud v prostoru C1 vezmu jenom supremovou normu, tj. stejnou normu jako v C, spojitost evidentne neplati kvuli ↑ vlado_bb:
Offline
#24 16. 04. 2019 14:16 — Editoval Rumburak (17. 04. 2019 10:27)
Re: Spojitost zobrazení
↑ Flaky:
Jen rozvedu nápovědu kolegy ↑ vlado_bb: :
EDIT.
Zkoumej funkci  pro různá
pro různá  .
.
Offline
#25 16. 04. 2019 15:02
Re: Spojitost zobrazení
↑ Rumburak: Len upresnim - nejde o napovedu, ale uplne riesenie. Nevadi, verim ze zadavatel bude moct prezit radost z uspechu pri rieseni inych problemov. Chcel som mu to umoznit, nic viac.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spojitost zobrazení (TOTO TÉMA JE VYŘEŠENÉ)

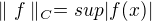 , kde
, kde ![kopírovat do textarea $x\in [0,1]$](/mathtex/78/78bb3465294c0a7bd59c6a1cdea9a087.gif) ano?
ano? nie je funkcia definovana na
nie je funkcia definovana na ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) .
.