Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2019 10:47 — Editoval stuart clark (11. 04. 2019 10:48)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
function and limit
If  and
and  is differntiable and increasing function
is differntiable and increasing function
Then value of 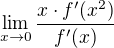 is
is
Offline
#2 11. 04. 2019 23:39
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: function and limit
Hi, everything seems to me that it should be
even for nonincreasing functions..."Máte úhel beta." "No to nemám."
Offline
#3 14. 04. 2019 10:17
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: function and limit
Thanks ↑ check_drummer:
but in answer, left side limit does not exists and right side limit 
Offline
#4 15. 04. 2019 12:30
Re: function and limit
↑ stuart clark: Then there is a mistake in the answer key. Consider f(x)=x^3, then f'(x)=3x^2, f'(x^2)=3x^4 and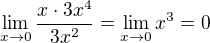 .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#7 17. 04. 2019 12:21
Re: function and limit
↑ Bati: nothing, it just demonstrates that ↑ stuart clark: 's answer is wrong.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 17. 04. 2019 16:00
Re: function and limit
↑ Bati:
If I see a statement such as ↑ stuart clark: and there is a free variable (f), then I automatically consider it a shortcut of longer statement: (forall f) (the original statement).
Perhaps ↑ byk7: understants it the same way.
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 17. 04. 2019 16:57
Re: function and limit
↑ Andrejka3:
yes, but what im saying that the answer in the key might be just poorly stated..but if it is actually true that there is a function for which the limit doesnt exist, its much mire interesting than saying for some f the limit is 0 (which is obvious).
Somebody should really solve this and end this discussion :)
Offline
#11 18. 04. 2019 13:03
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: function and limit
Thanks to all members .Yes you all are right my answer is wrong
Offline