Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 30. 04. 2019 02:25 — Editoval laszky (30. 04. 2019 02:29)
Re: Integration Inequality
↑ stuart clark:
Hi. Is it correct that there can be square roots of negative values? For instance, for 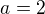 ,
,  we obtain
we obtain 
Hence, absolute value of complex number has to be considered for 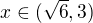 .
.
Offline
#3 30. 04. 2019 16:39
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Integration Inequality
I will conform it from original source ↑ laszky:
Offline
#5 18. 05. 2019 16:36
Re: Integration Inequality
↑ stuart clark:
Hi, the expressions under the square root are not the same as you have written.
Offline
#6 21. 05. 2019 05:29
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Integration Inequality
Yes ↑ laszky: you are Right
Offline