Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 08. 05. 2019 12:21 — Editoval stuart clark (09. 05. 2019 17:11)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Maximum value
Thanks friends Got it.
Let 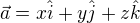 and
and 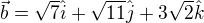
Now Using 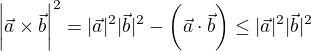
So 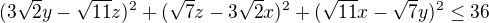
Equality hold when 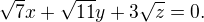
Offline
#3 08. 05. 2019 12:33 — Editoval stuart clark (08. 05. 2019 12:55)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Maximum value
I have a doubt on that problem
Show that for any positive integer 

Plesse have a look on that problem. Thanks
Offline
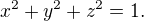 Then maximum value of
Then maximum value of 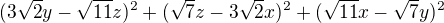 is
is