Matematické Fórum

NeuRotiCk

Dobrý mám příklad na vázané extrémy, nejsem si jistý jestli postupuju správně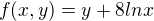
$f(x,y)=y+8lnx$ s vazbou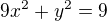 $9x^{2}+y^{2}=9$
vazbu převedu do tvaru 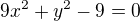$9x^{2}+y^{2}-9=0$
$L(x,y,\lambda ) = y+8lnx +\lambda (9x^{2}+y^{2}-9)$
derivace podle x
$L_{x}(x,y,\lambda ) = 8/x + 18\lambda x$
derivace podle y
$L_{y}(x,y,\lambda ) = 1+2\lambda y$
derivace podle lambdy
$L_{\lambda }(x,y,\lambda ) = 9x^{2}+y^{2}-9$

Teď jsem hledal stacionární body ze soustavy rovnic, které vyšly z těch derivací:
$8/x+18\lambda x=0$
$1+2\lambda y=0$
$9x^{2}+y^{2}-9=0$

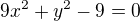
A teď právě nevím jestli sem to mohl udělat takhle:
z druhé rovnice sem vyjádřil 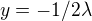$y=-1/2\lambda$
a z první sem pak našel výraz: $18\lambda x=-8/x\Rightarrow \lambda =-4/9x^{2}\Rightarrow 9x^{2}=-4/\lambda$
A tyhle dva výrazy sem dosadil do té poslední, třetí rovnice a vyšlo mě:
$-4/\lambda +(-1/2\lambda )^{2}-9=0\Rightarrow 9\lambda ^{2}+4\lambda -1/4$
Vypočítal sem normálně kvadratickou rovnici a vyšly mě kořeny: $\lambda _{1}=1/18$ a $\lambda _{2}=-1/2$
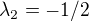
A tyhle dva body sem dosadil do toho vyjádření, co sem udělal nahoře a našel sem výsledný body:
$[±\sqrt{8/9},1,-1/2]$ a pak sem pokračoval dál, jak je tomu zvykem, determinant mě vyšel $<0$ takže tam nenastal žádnej extrém.
Ale nejsem si jistej tím vyjádřením 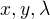$x,y,\lambda$ .
Předem děkuji za jakoukoliv odpověď.