Matematické Fórum

NeuRotiCk

Dobrý den, mám tu jeden příklad na počáteční úlohu, co jsme probírali na cvičení, ale netuším jak jsme se dobrali k určité věci.
Zadání:
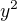$y^{2}+6y^{1}+9y=0$ kde $y^{2}$ je druhá derivace a $6y^{1}$ je derivace 1.
Tohle vím jak spočítat, dělali jsme to přes tu lambdu, ale pak jsme tam měli ještě $y(0) =2, y^{1}(0) =-1$ kde je zase $y^{1}(0) =-1$ hodnota v první derivaci.
Ale tohle není součástí zadání, jak na to přijdu?
Předem děkuji za jakoukoliv odpověď.

NeuRotiCk · 11. 05. 2019 11:35

Pro úplnost teda můžu ještě doplnit spočítané: $y(x)=c_{1}\cdot e^{-3x}+c_{2}\cdot x\cdot e^{-3x}$ ; kde $c_{1},c_{2}$ náleží všem reálným číslům.

NeuRotiCk

Teď, když se divám na nějaké zkouškové testy, tak jim tam dal y(0) = hodnota, ale nám na cvičení říkal, že na to máme přijít, tak teď nevím teda.

krakonoš · 11. 05. 2019 12:30

↑ NeuRotiCk:
Ahoj.
Ty podminky y(0).... by mely byt soucasti zadani.Z nich se podle me urci prave ty c1,c2

NeuRotiCk · 11. 05. 2019 12:40

To jsem si myslel taky, ale není tomu tak, on nám na cvičení říkal, že se to dá odvodit, zadal jen tu počáteční hodnotu, to je vše, u zkoušky má zadané y(0)= ale nemá zadanou hodnotu v té první derivaci.

MichalAld · 11. 05. 2019 12:40

1) Ty konstanty C1, C2 nemusejí být jen reálné, mohou být obecně i komplexní. To může být nesmírně užitečné, když vyjdou komplexní ty $\lambda$ - protože to pak vede na harmonické funkce.

2) Na počáteční podmínky nelze nějak "přijít", pokud nejsou zadány, tak ty konstanty C1, C2 prostě neurčíme.

NeuRotiCk · 11. 05. 2019 12:43

Je pravda, že na zkoušce teda nemají rovnice vyššího řádu ale pouze pro první derivaci a tam je teda jenom jedna konstanta a tu mají zadanou ve formě y(0)=
Ale u těch vyšších řádů nám zadal jen tu počáteční úlohu jak sem psal, y(0) = a hodnotu v první derivaci odvodil.

NeuRotiCk · 11. 05. 2019 12:46

Ale je dost možný, že sem ho nějak přeslechl, vím, že říkal že se to dá logicky odvodit, možná čerpal ze zkušenosti a věděl jak na to. Děkuju všem.

MichalAld · 11. 05. 2019 13:07

Pokud to z něčeho odvodil, je také třeba vědět z čeho. Ony také existují jiné podmínky než ty počáteční, třeba mohou být zadány okrajové podmínky...

krakonoš

Mozna se tim myslelo,ze pouzijes podminku y(0) rovno -1,nasledne dostanes nejakou informaci o jednom z clenu c1,c2.To jiz zname dosadis do rovnice a pak teprve derivujes y()......a pouzijes tu druhou podminku.
Pokud neznas podminky,tak podle nasobnosti korene jsi maximalne schopny rici,zda jde o ciselnou kombinaci nebo linearni....

Matematické Fórum

#1 11. 05. 2019 11:27 — Editoval NeuRotiCk (11. 05. 2019 11:30)

počáteční úloha pro rovnici vyššího řádu

#2 11. 05. 2019 11:35

Re: počáteční úloha pro rovnici vyššího řádu

#3 11. 05. 2019 12:02 — Editoval NeuRotiCk (11. 05. 2019 12:41)

Re: počáteční úloha pro rovnici vyššího řádu

#4 11. 05. 2019 12:30

Re: počáteční úloha pro rovnici vyššího řádu

#5 11. 05. 2019 12:40

Re: počáteční úloha pro rovnici vyššího řádu

#6 11. 05. 2019 12:40

Re: počáteční úloha pro rovnici vyššího řádu

#7 11. 05. 2019 12:43

Re: počáteční úloha pro rovnici vyššího řádu

#8 11. 05. 2019 12:46

Re: počáteční úloha pro rovnici vyššího řádu

#9 11. 05. 2019 13:07

Re: počáteční úloha pro rovnici vyššího řádu

#10 11. 05. 2019 13:15 — Editoval krakonoš (11. 05. 2019 13:22)

Re: počáteční úloha pro rovnici vyššího řádu

Zápatí