Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Sumy s kombinačními čísly (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 05. 2019 22:29
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Sumy s kombinačními čísly
Ahoj, dokažte, že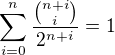 .
.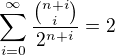 .
.
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) check_drummer)
#2 15. 05. 2019 02:24 — Editoval vanok (15. 05. 2019 02:25) Příspěvek uživatele vanok byl skryt uživatelem vanok.
#3 03. 11. 2019 01:12
Re: Sumy s kombinačními čísly
↑ check_drummer:
Ahoj, to uz tu je tak dlouho nevyreseny? Tak ja bych zkusil napr.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Sumy s kombinačními čísly (TOTO TÉMA JE VYŘEŠENÉ)
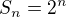 , kde
, kde 
![kopírovat do textarea $S_n-S_{n-1} = \sum_{i=0}^n\frac{\binom{n+i}{i}}{2^i}-\sum_{i=0}^{n-1}\frac{\binom{n-1+i}{i}}{2^i} = \frac{\binom{2n}{n}}{2^n} + \sum_{i=0}^{n-1}\frac{1}{2^i}\left[\binom{n+i}{i}-\binom{n-1+i}{i}\right] = $](/mathtex/09/09522a8b688e341e723498f31180f329.gif)
![kopírovat do textarea $= \frac{\binom{2n}{n}}{2^n} + \sum_{i=1}^{n-1}\frac{1}{2^i}\binom{n-1+i}{i-1} = \frac{\binom{2n}{n}}{2^n} + \frac{1}{2}\sum_{i=0}^{n-2}\binom{n-2+i}{i} = \frac{\binom{2n}{n}}{2^n} + \frac{1}{2}\left[S_n- \frac{\binom{2n-1}{n-1}}{2^{n-1}}- \frac{\binom{2n}{2}}{2^n}\right]$](/mathtex/37/37a29465bb7443e0c4fc8822685b111f.gif)
![kopírovat do textarea $\frac{1}{2}S_n-S_{n-1}=\frac{1}{2^{n+1}}\left[\binom{2n}{n}-2\binom{2n-1}{n-1}\right] =\frac{1}{2^{n+1}}\left[\binom{2n}{n}-\binom{2n-1}{n-1}-\binom{2n-1}{n}\right] = 0$](/mathtex/cc/cc366f57259f98edd463f8ee536f88fe.gif)
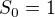 , je
, je 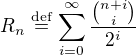 a ziskame rovnou (viz vyse)
a ziskame rovnou (viz vyse)  , takze
, takze  . Zaroven
. Zaroven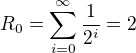 , takze
, takze  .
.