Matematické Fórum

NeuRotiCk · 17. 05. 2019 12:25

Dobrý den, nevím si rady s touhle DR:
y’ +y/2 = x/π ; y(2) = 0
y’ = x/π - y/2
já sem udělal substituci: $u=-y/2$ to je jinak $u(x)=-y(x)/2 \Rightarrow y(x) = -2\cdot u(x)$ ale potom, co to zderivuju tak by mi vyšlo že derivace $y(x) = 0$ a pak by mi vyšla DR ve tvaru $0=x/\pi +2u(x)/2 \Rightarrow u(x)+x/\pi =0$
Ale nějak se mi to nezdá, nevím jak bych měl pokračovat, jestli sem udělal dobře substituci?
Derivuje se tam podle x, tím pádem si myslím, že ta derivace je správně a vyjde 0, ale celý mi to nijak nesedí.
Kdyby mě někdo dokázal natuknout, byl bych vděčný.

laszky · 17. 05. 2019 12:59

↑ NeuRotiCk:

Ahoj, jeden ze zpusobu je vyuzit toho, ze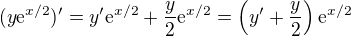

$(y\mathrm{e}^{x/2})' = y'\mathrm{e}^{x/2} + \frac{y}{2}\mathrm{e}^{x/2} = \left(y'+\frac{y}{2}\right)\mathrm{e}^{x/2}$ ,

takze kdyz puvodni rovnici vynasobis $\mathrm{e}^{x/2}$ , ziskas vztah

$(y\mathrm{e}^{x/2})' = \frac{x}{\pi}\,\mathrm{e}^{x/2}$ .

Jeho zintegrovanim pak dostanes

$y\mathrm{e}^{x/2} = \int \frac{x}{\pi}\,\mathrm{e}^{x/2} \, \mathrm{d}x + C$

Z toho uz muzes dopocitat reseni.

NeuRotiCk · 17. 05. 2019 13:37

Tak na tohle bych, nepřišel, děkuju mockrát za pomoc.

Matematické Fórum

#1 17. 05. 2019 12:25

diferenciální rovnice

#2 17. 05. 2019 12:59

Re: diferenciální rovnice

#3 17. 05. 2019 13:37

Re: diferenciální rovnice

Zápatí