Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 09. 2009 18:51
lokální extrémy
x^2y+yy^2-3xy ... počítám to tak že si to zderivuju podle x a podle y -- mam dvě rovnice položim je rovno nule a chci si vyjádřit x a y ale to mi nejde at se snažim jak se snažim tak se mi tam pletou jiný čísla podle toho jak vyjadřuju a kam pak zpátky dosazuju nevíc včem je problém?
Offline
#3 01. 09. 2009 19:27
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: lokální extrémy
↑ silr:
Mozna resite špatné rovnice, treba je sem napiste a napiste postup, jak to resite. Nekdo vam urcite ukaze, kde mate chybu. Tim se naucite mnohem vic nez prohlizenim vzorového řešení.
Offline
#4 02. 09. 2009 03:26 — Editoval silr (02. 09. 2009 03:27)
Re: lokální extrémy
tim postupem si to osvěžíme všichni to je pravda .... když tedy x=y tak si můžu zvolit libovolný?? já to nemůžu nějak to řešení vykoukat -- každopádně až budu znát x a y to je podezřelý bod nebo jích může být i víc --- ty si dosadim do derivací 1 2 3 4 a následně do matice --- a vypočítám si determinanty a podle uvedených pravidel se rozhodnu ?? posupově by to mělo být správně ne??
Offline
#5 02. 09. 2009 08:43
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: lokální extrémy
1. jak z 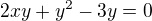 dostanu
dostanu  ? A podobne: jak presne dostanu
? A podobne: jak presne dostanu 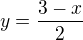 ?
?
2. jak z  a
a 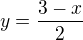 dostanu, ze
dostanu, ze  ? (Ona to nakonec je pravda, ale dokonce z techto dvou rovnic plyne
? (Ona to nakonec je pravda, ale dokonce z techto dvou rovnic plyne  - soustava dvou lineárních rovnic o dvou neznámých)
- soustava dvou lineárních rovnic o dvou neznámých)
Stacionární body jsou [0,0];[0,3];[3,0];[1,1]. Pokus si pořádně rozepíšete tu první otázku, jistíte, kde jste potratil ty první tři body a pokud si pořádně vyřešíte tu soustavu, najdete ten poslední.
Stačilo?
Offline
#6 02. 09. 2009 12:22
Re: lokální extrémy
to vyjádření y a x chápu ... ale pak jsem měl problém když jsem zjištoval ty stacionární body ... když jsem si vyjádřil x a y a pak následně dosazoval do rovnic tak mi tam vycházeli protichůdná čísla jak jsem dosazoval a neskutečně jsem se do toho zeplet (muj zkouškovej příklad) tak bych potřeboval rozebrat přesně postup jak zjistit ty všechny stacionární body??
Offline
#7 02. 09. 2009 12:34 — Editoval kaja(z_hajovny) (02. 09. 2009 12:35)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: lokální extrémy

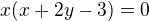
Součin je nula právě tehdy, když některý ze součinitelů je nula (inteligent by řekl, že to je proto, že pracujeme v oboru integrity). No a u nás mají bý tnula hned dva součiny. Jsou celkem 4 kombinace:
1. x=0 a y=0
2. x=0 a 2x+y-3=0
3. y=0 a ....
4 .......
jasné?
Offline
#9 06. 09. 2009 09:24
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: lokální extrémy
tak jeste jinak: z první rovnice vidím že buď y=0 nebo y=3-2x
nechť nejprve y=0. V druhé rovnici mám x(x-3)=0 a buď x=0 nebo x=3
necť nyní y=3-2x. V druhé rovnici mám x(x+6-4x-3)=0, tj. x(3-3x)=0 a buď x=0 nebo x=1, Protože y=3-2x, tak volba x=0 dává y=3-0=3 a volba x=1 dává y=3-2*1=1
Jasan?
Offline



 .
. , tak
, tak