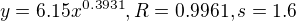Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 09. 2019 22:07
Proložení tabelovaných dat křivkou - ale jakou?
Já se s tím marně trápím, zatímco někdo zkušenější třeba mrkne a hned ví :-) Neměl byste prosím někdo tip, jakou funkci bych měl zvolit pro proložení tabelovaných dat křivkou? Data jsou modře, červeně je můj pokus o proložení polynomem druhého a zeleně třetího stupně (metodou nejmenších čtverců). Už od pohledu je vidět, že to moc nesedí, hlavně začátek grafu.
Já bych při tom potřeboval, aby proložení vypadalo nějak takhle (ručně proložené splinem v grafickém programu). Takhle by to vyhovovalo i přesností, ale neumím to udělat jako funkci y=f(x). 
Konkrétní data vypadají například takhle (hodnoty y se tam občas opakují, protože jsou empiricky zjištěné a zaokrouhlené):
data_x = [1.7, 4.2, 7.7, 11.8, 15.9, 20.8, 26.8, 34.6, 44.7, 57, 72.1, 89.4, 109.5, 129.6, 149.7, 169.7, 189.7, 212.1, 237.2, 264.6, 297, 334.4, 376.8, 424.3, 474.3]
data_y = [6, 12, 15, 18, 18, 22, 22, 26, 26, 32, 32, 37, 37, 43, 43, 43, 50, 50, 50, 56, 56, 62, 62, 68, 68]
Děkuji za případné rady jak na to :-)
Offline
#2 22. 09. 2019 22:26
- check_drummer

- Příspěvky: 5178
- Reputace: 106
Re: Proložení tabelovaných dat křivkou - ale jakou?
Ahoj, křivek by se dalo najít hodně - podstatné asi bude jak jsou data získáma, tj. co ty naměřené hodnoty vyjadřují. Pak by se dala stanovit nějaká obecná závislost a konkrétní konstanty té závislosti by se pak mohly stanovit metodou nejmenších čtverců.
"Máte úhel beta." "No to nemám."
Offline
#3 22. 09. 2019 22:38
Re: Proložení tabelovaných dat křivkou - ale jakou?
Jo jo, je třeba vědět, co data představují.
Jinak ta křivka co jsi namaloval mi připadá jako druhá (nebo nějaká jiná) odmocnina.
A nebo logaritmická funkce.
Polynom N-tého stupně není obecně příliš vhodný na prokládání dat zatížených takovýmit velkými chybami - má tendenci se kvůli tomu "rozvlnit". Je třeba použít křivku s co nejmenším počtem stupňů volnosti.
Taky je dobrý trik to vynést do grafu s logaritmickou stupnicí - spousta funkcí se tam změní na přímky...
Offline
#4 22. 09. 2019 22:56 — Editoval Aleš13 (22. 09. 2019 22:57)
Re: Proložení tabelovaných dat křivkou - ale jakou?
Dík. Data jsou ze strojírenských tabulek, udávají doporučenou vůli hřídele v díře. X je průměr hřídele v mm, Y je vůle v tisícinách mm. Jsou tabelované pro různá použití a stupně přesnosti výroby a já bych to rád aproximoval nějakou ne moc složitou funkcí, aby se to dalo naprogramovat třeba do makra. Myslel jsem si, že tohle už muselo udělat tisíc lidí přede mnou, ale nic jsem nenašel :-)
Offline
#5 22. 09. 2019 23:30 — Editoval Ferdish (22. 09. 2019 23:31)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Proložení tabelovaných dat křivkou - ale jakou?
↑ Aleš13:
Strojár nie som, ale podľa profilu dát to vyzerá na závislosť podľa mocninovej funkcie s racionálnym, eventuálne reálnym exponentom.
Offline
#7 23. 09. 2019 10:10
Re: Proložení tabelovaných dat křivkou - ale jakou?
↑ Honzc:Díky, večer si s tím pořádně pohraju :-)
Ty hodnoty průměrů jsou středy intervalů podle tabulek. Jsou to geometrické průměry, nevím proč, ale v ISO normě píšou, že pro zjemňování dělení se má použít geometrický průměr :-)
Offline
#8 23. 09. 2019 19:45
Re: Proložení tabelovaných dat křivkou - ale jakou?
Ale jinak - problémy tohoto typu se programují tak, že si do programu uděláš tu tabulku cos napsal sem a pak mezi sousedními body děláš tu interpolaci (až v okamžiku, kdy to potřebuješ počítat).
Pak je taky otázka, jestli ten geometrický průměr se nemá použít na tu toleranci a né na průměr hřídele.
Protože je to blbost, aby to takto hopsalo.
Offline
#9 23. 09. 2019 20:28 — Editoval Aleš13 (23. 09. 2019 20:30)
Re: Proložení tabelovaných dat křivkou - ale jakou?
↑ MichalAld:
Jasně, tak to mám naprogramovaný teď, ale přijde mi to takový humpolácký. Navíc ta data si přímo říkají o vyhlazení, ono je to takovéhle rozskákané (a místy je tam i porušená monotónie, což nemá žádnou oporu v realitě) i když použiju hranice intervalů přesně podle té normy. Ale chápu to, ta data vznikla v předminulém století, občas tam někdo špatně šoupnul logaritmickým pravítkem a bylo to. A od té doby je nikdo neměnil. Teď si s tím hraju a vypadá to, že to opravdu půjde "uhezkat" těmi mocninnými křivkami, možná to dokonce i nějak odpovídá fyzikální povaze těch vůlí a přesahů :-)
Offline