Matematické Fórum

karelpavlis · 08. 10. 2019 12:43

Dobrý den,
chtěl bych si provést důkaz, že těžiště trojúhleníku dělí těžnice na třetinu a dvě třetiny.

laszky · 08. 10. 2019 13:24 — Editoval laszky (09. 10. 2019 14:57)

↑ karelpavlis:

Ahoj, pokud je definice teziste $T=\frac{A+B+C}{3}$ a napr. rovnice teznice na stranu c $t_c(\alpha)=C+\alpha\left(\frac{A+B}{2}-C\right),\ \alpha\in[0,1]$ ,
staci vyresit rovnici 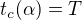$t_c(\alpha)=T$ a zjistit,ze 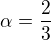$\alpha=\frac{2}{3}$ . Takze teziste se nachazi ve dvou tretinach delky teznice.

krakonoš

↑ karelpavlis:
Mně příjde, že k těžišti se dostaneme tak, že uděláme v trojúhelníku střední příčky a tento proces opakujeme do nekonečna.Vyrazí-li bod z vrcholu zadaného trojúhelníku po těžnici až na protější stranu, urazí dráhu rovnu 1, pak se pohybuje zpět od vrcholu druhého trojúhelníku( toho polovičního vytvořeného ze středních příček) a běží opět k protější straně. Urazí tak dráhu -1/2, pak opět běží od vrcholu již toho třetího trojúhelníku knprotější straně, jeho dráha bude rovna +1/4 atd....
Dostaneme tak součet nekoneçné řady 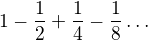$1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}\ldots$ , jejíž souçet je 2/3

vanok · 08. 10. 2019 19:44

Ahoj ↑ karelpavlis:,
Jedno ine riesenie.
Ako prve mozes dokazat, ze taznice delia jeden trojuholnik na sest trojuholnikov rovnakej plochy.
A to potom vyuzi na dokaz tvojho problemu.

krakonoš

↑ karelpavlis:
Ten poměr 2:1 lze dokázat rychle přímo (i bez použití rovnosti ploch trojúhelníků).
Udělej si u trojúhelníku ABC střední příčku rovnoběžnou se stranou AB, bude s ní rovnoběžná a bude mít poloviční velikost. Dále si udělej střední příčku trojúhelníku ABT, kde T je těžiště. Opět bude střední příčka rovnoběžná a bude mít poloviční velikost. Tedy obě střední príčky budou shodné a rovnoběžné.Vyplyne z toho shodnost dvou malých trojúhelníků , u prvního je jednou stranou střední příčka tojúhelníku ABC a protilehlý vrchol je T a u druhého střední příčka trojúhelníku ABT a protilehlý vrchol T. Z toho už pak vyplyne pomět 2:1.
To že šest trojúhelníků má shodnou plochu, lze brát jako naopak důsledek tohoto poměru. Střední příčky zajistí poloviční , čtvrtinové plochy.....Jak ale dosáhneme dělitelnosti třemi ? Vidím to pouze z postupu, kde dokazujeme, že těžnice se půlí v poměru 2:1, možná existuje nějaký fikanější způsob , jak vidět shodnost ploch těch 6 trojúhelníků, aniž bychom tento poměr použili, zatím to ale nevidím.

vanok · 09. 10. 2019 11:22 — Editoval vanok (09. 10. 2019 11:48)

Poznamka.
Maly problem a vela moznosti riesenia.
↑ karelpavlis: nereaguje, tak ani nevieme ci vobec cital nase reakcie.
Mozno by sa mu pacil a pristup fyzikov.
Presnejsie : vyuzit pojem barycentra a jeho asociativitu.
[ napisem myslienku schematicky tu: bodom A, B, C sa priradi coeficient 1; tzv vaha, barycentre ((B,1);(C,1)) je bod ( M,2) a bar((A,1),(B,1),(C ,1))=bar ((A,1),(M,2))=. ...]
Pochopitelne, pojem barycentrickych suradnic sa pouziva aj v matematike, no pochybujem, ze dnesny stredoskolaci o tom poculi.
Atd ....
Inac, co sa tyka stredoskolaka, najpratickejsia (co sa tyka analytickej geometrie) metoda je ta v #2 lebo umoznuje pocitaj suradnice taziska.
A tiez asi kazdy stredoskolak vie, ze definicia kolegu ↑ laszky: ( pozdravujem) je ekvivalentna z
$\vec {TA}+\vec{TB}+\vec{TC}=\vec 0$ .... (aka pekna « symetria »).’’

krakonoš · 09. 10. 2019 11:36

↑ vanok:
Ahoj
Ten první můj důkaz je jen z mé hlavy, ten druhý z literatury.Co se týče toho, že z rovnosti 6 ploch trojúhelníků plyne poměr 2:1 , jsem našla na internetu -Khamova škola, kde se odkazují na dříve dokázanou stejnou velikost ploch.Toto dřívější video ale už jsem nikde nenašla. Je mi fakt divná ta dělitelnost třemi, co jiného než ten poměr by to zajistilo, aby se ten důkaz dal brát i obráceně.

vanok · 09. 10. 2019 11:45

↑ krakonoš:,
Mali by sme o tom otvorit diskuziu v didaktickom vlakne.
Dalo by sa o tom povedat.
V niecom je lepsie pouzit symetricke vlasnosti v takych dokazoch, lebo ide o dokazy, kde vsetki body ( vrcholov trojuholnika) su rovnocenne. ..’
Ale ako vidis autor otazky zatial nereagoval.
Tak naco tu pokracovat.

karelpavlis · 09. 10. 2019 11:47

Četl jsem, díky moc za všechny nápady. Jen jsem ještě nestihl zareagovat.
Ten součet nekonečné řady je vtipný a asi by mě to samotného nenapadlo.
Krakonošův druhý způsob bez počítání je zdá se jednodušší, ale ještě musím promyslet, proč jsou oba zmíněné trojúhelníky shodné...
Postup Laszkyho a barycentra jsou pro mě zatím hůře uchopitelné... :-(

krakonoš · 09. 10. 2019 12:06

↑ vanok:
Těžiště svým způsobem odpovídá střední hodnotě, jedině kolega laszki bere rovné váhy, což odpovídá (A+B+C)/3.
Tvůj součet vektorů, které dají nulový vektor by při podělení třemi podle mě odpovídal E(X-EX)=0

vanok · 09. 10. 2019 12:51 — Editoval vanok (09. 10. 2019 13:14)

↑ krakonoš:,
Co pise kolega je vlastne vektorova rovnica napisana v suradnicovom systeme. A ta dohoda je pouzivana aj na strednych skolach .
Ekvivalencia oboch rovnosti sa dokazuje vdaka Chasles-ovej relacii.( angl. hovoria aj relacii od Nomizu a Sasaki). https://fr.wikipedia.org/wiki/Relation_de_Chasles
Staci?

Tvoj suvis zo statistikou som zatial nikdy neanalyzoval.

krakonoš · 09. 10. 2019 13:10

↑ vanok:
Díky.
Já nemám žádné připomínky důkazu, který uvádí laszki, ten postup je naprosto vpořádku, naopak zde poukazuji na jistou souvislost se statistikou.
Já jen měla otázky k rovnosti ploch těch 6 trojúhelníků, zajímala by mě ekvivalence těch dvou věci t.j. rovnost ploch a poměr 2:1. Zatím vidím jen implikaci.

vanok · 09. 10. 2019 13:27

↑ krakonoš:
Ukazat rovnost ploch to vidis?
A vlastne vsetko je vyuzitie, ze plocha trojuholnika je ( baza x vyska)/2

vanok · 09. 10. 2019 13:36 — Editoval vanok (09. 10. 2019 13:45)

↑ krakonoš:,
Este sa mozes pohrat aj z tymto obrazkom ( najdes aj ine myslienky)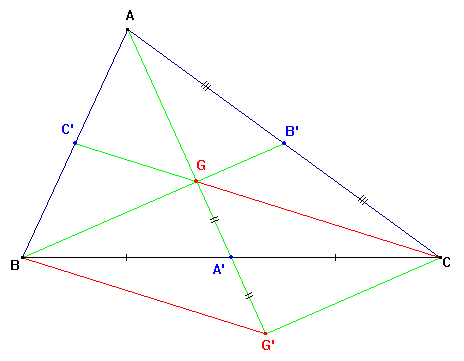
//forum.matweb.cz/upload3/img/2019-10/20666_46743393-621E-40D3-9939-276A44992D7D.gif

G oznacuje tazisko (Gravitacne centrum).

Ale zda sa, ze takyto obrazok ako aj dokaz danej vlasnosti som videl uz na zakladnej skole. ( ci sa este stale nieco take uci na skolach neviem, mozno osnovy sa ozaj zmenili? Za 55 rokov je to mozne. )

krakonoš · 09. 10. 2019 13:55

[re]p591757|vanok[/re
Díky moc.
Dívala jsem se na běžný obrázek s těžnicemi, ale na první pohled jsem viděla jen čtvrtinové a poloviční plochy než má zadaný trojúhelník.Tak jsem si myslela,že máš na tu rovnost ploch důkaz., když jsi to sám navrhoval,jen mě zajímal, nic víc.

vanok · 09. 10. 2019 13:56

Spomienky k obrazku.

Nech AA’ a BB’ su dve taznice trojuholnika ABC a G’ je symetricky bod bodu G relativne k A’.
BGCG je rovnobeznik. A tak (BB') / /(G'C);
V trojuholniku ACG', (GB') prechadza stredom z [AC] a (GB') // (G'C);
G je tak stred z [AG'];
GA je dvojnasobok z GA' cize GA = 2GA'.

gadgetka

Zdravím vespolek :) a přidávám také jeden důkaz:

//forum.matweb.cz/upload3/img/2019-10/22329_graf_0624.png

Edit: :D vanok byl rychlejší ... jen je to jinak položené... ;)

vanok · 09. 10. 2019 14:14 — Editoval vanok (09. 10. 2019 15:59)

↑ krakonoš:
Ty ma chces za kazdu cenu chces poslat do spomienok zo ZS.

Vsak som pisal 1/6 plochy daneho trojuholnika.
Nastien dokazu.
Pouzijem oznacenie obrazku.
Trojuholniky GBA’ a GCA’ maju rovnakej dlhe bazy a rovnaku vysku vzladom citovanym bazam. Tak su rovnoplosne.
Trojuholniky GBC’ a GBA’ ....ta ista metoda ale najprv narysuj priecku A’C’ a vyuzi ju.....

Vsetko je ozaj v tomto hyperjednoduche. Ci nie?

Teraz na dokaz, ze |GA|= 2|GA’ |=(2/3).|AA’| (*) pouzit, ze
plocha(GBA)= 2.plocha(GBA’) (cf. predosle riadky)
A, ze plocha (GBA)= (1/2).|GA|v ; plocha(GBA’)=(1/2). |GA’|v
(v je vyska z B , ktora je ta ista pre oba trojuholniky) .
[ v poslednej rovnosti vyuzijes tu prvu cast dokazu!].

vanok · 09. 10. 2019 14:21 — Editoval vanok (09. 10. 2019 14:30)

Pozdravujem ↑ gadgetka:,

Ano, aj takto sa to da z organizivat.
( to su tvoje spomienky zo ZS ci zo SS?)

No robime tu ozaj didakticku diskuziu.

Mohli by sme este pokracovat v afinnej geometrii ... no ale ozaj tu nie ( ostanme najviac na urovni SS)

vanok · 09. 10. 2019 14:27

Ahoj ↑ karelpavlis:,
Dakujem za tvoju reakciu.
Tak ako sa zda, tato diskuzia ta zaujala.
Myslis, ze je to uzitocne a ty to pomoze k pochopeniu tvojho problemu?

karelpavlis

Nestačím se divit, jak se toto téma tady rozjelo :-)
Chvíli mi zabere prokousat se všemi příspěvky. Afinní geometrii však - pardon - zřejmě vynechám...

krakonoš · 09. 10. 2019 14:39

↑ gadgetka:
Díky
Také zajímavý důkaz, jsou tam hezky vidět půlícíse úhlopříčky dvou rovnoběžníků.

krakonoš

↑ vanok:
Obrázek je krásný i barevně, hezká didaktická pomůcka.
Na základě rovnoběžníku BG'GC a toho, že GB' je střední příčkou trojúhelníka lze dokázat, že |GG'|=|GA|, z toho bezprostředně plyne náš poměr 2:1.
Tuto rovnost bychom museli použít i k důkazu rovnosti ploch tří dvojic trojúhelníků, kde jejich plocha (každé dvojice)je vždy stejná jako polovina plochy rovnoběžníku.
V jednotlivé dvojici trojúhelníků mají oba trojúhelníky stejný obsah, protože mají stejně velkou výšku i základnu.Takže těch 6 trojúhelníků má opravdu stejný obsah.Nelze však na základě tohoto faktu dokazovat poměr 2:1, protože k důkazu rovnosti ploch byla použita rovnost|GG'|=|GA|, jejím důsledkem je vlastně náš poměr2:1. Podobně důsledkem této rovnosti je shodnost obsahu ploch šesti trojúhelníků. Takže mi příjde neekonomické dokazovat nejprve shodnost ploch a s pomocí výšky pak dopočítávat základny a poměr 2:1., jako to dělá Khanova škola.
Jedině že by měli nějaký úplně jiný důkaz na shodnost ploch, který s tou rovností nemánic společného, ale o tom pochybuji.

vanok · 09. 10. 2019 16:29 — Editoval vanok (09. 10. 2019 16:34)

↑ krakonoš:,
Ten obrazok pouzil len pre oznacenia.
V dokaze #18 nikde nie je pouzite G’. ( pozri pozornejsie ten dokaz ).
|GA’|=(1/3).|AA’| ( vdaka comu? .... uz vidis 3 trojuholniky a jeden).

Edit. Miesas dva dokazy. Ten zo ZS #16 a ten z trojuholnikmi#18.

vanok · 09. 10. 2019 16:57

↑ krakonoš:,
Co myslis, o tomto cviceni?

Aky je pomer plochy jedneho daneho trojuholnika a plochy trojuholnika ktoreho strany su dlzky taznic daneho trojuholnika?

Matematické Fórum

#1 08. 10. 2019 12:43

Těžnice trojúhleníku se protínají ve třetině

#2 08. 10. 2019 13:24 — Editoval laszky (09. 10. 2019 14:57)

Re: Těžnice trojúhleníku se protínají ve třetině

#3 08. 10. 2019 14:07 — Editoval krakonoš (08. 10. 2019 14:10)

Re: Těžnice trojúhleníku se protínají ve třetině

#4 08. 10. 2019 19:44

Re: Těžnice trojúhleníku se protínají ve třetině

#5 09. 10. 2019 09:58 — Editoval krakonoš (09. 10. 2019 11:16)

Re: Těžnice trojúhleníku se protínají ve třetině

#6 09. 10. 2019 11:22 — Editoval vanok (09. 10. 2019 11:48)

Re: Těžnice trojúhleníku se protínají ve třetině

#7 09. 10. 2019 11:36

Re: Těžnice trojúhleníku se protínají ve třetině

#8 09. 10. 2019 11:45

Re: Těžnice trojúhleníku se protínají ve třetině

#9 09. 10. 2019 11:47

Re: Těžnice trojúhleníku se protínají ve třetině

#10 09. 10. 2019 12:06

Re: Těžnice trojúhleníku se protínají ve třetině

#11 09. 10. 2019 12:51 — Editoval vanok (09. 10. 2019 13:14)

Re: Těžnice trojúhleníku se protínají ve třetině

#12 09. 10. 2019 13:10

Re: Těžnice trojúhleníku se protínají ve třetině

#13 09. 10. 2019 13:27

Re: Těžnice trojúhleníku se protínají ve třetině

#14 09. 10. 2019 13:36 — Editoval vanok (09. 10. 2019 13:45)

Re: Těžnice trojúhleníku se protínají ve třetině

#15 09. 10. 2019 13:55

Re: Těžnice trojúhleníku se protínají ve třetině

#16 09. 10. 2019 13:56

Re: Těžnice trojúhleníku se protínají ve třetině

#17 09. 10. 2019 14:03 — Editoval gadgetka (09. 10. 2019 14:06)

Re: Těžnice trojúhleníku se protínají ve třetině

#18 09. 10. 2019 14:14 — Editoval vanok (09. 10. 2019 15:59)

Re: Těžnice trojúhleníku se protínají ve třetině

#19 09. 10. 2019 14:21 — Editoval vanok (09. 10. 2019 14:30)

Re: Těžnice trojúhleníku se protínají ve třetině

#20 09. 10. 2019 14:27

Re: Těžnice trojúhleníku se protínají ve třetině

#21 09. 10. 2019 14:30 — Editoval karelpavlis (09. 10. 2019 14:31)

Re: Těžnice trojúhleníku se protínají ve třetině

#22 09. 10. 2019 14:39

Re: Těžnice trojúhleníku se protínají ve třetině

#23 09. 10. 2019 15:59 — Editoval krakonoš (09. 10. 2019 16:28)

Re: Těžnice trojúhleníku se protínají ve třetině

#24 09. 10. 2019 16:29 — Editoval vanok (09. 10. 2019 16:34)

Re: Těžnice trojúhleníku se protínají ve třetině

#25 09. 10. 2019 16:57

Re: Těžnice trojúhleníku se protínají ve třetině

Zápatí