Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 10. 2019 13:46
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Pravděpodobnost - kuličky
Ahoj, chci se poradit, zda jdu správně na následující úlohu:
Mám 3 černé, 3 bílé a 3 červené kuličky.
Bez vracení tahám 3 kuličky.
Jaká je pravděpodobnost, že:
a) padne od každé barvy 1
b) 2 barvy
c) všechny stejné barvy
Napadá mě tady hypergeometrické rozdělení: N=9, M=3, n=3 a x=1 pro a), výsledek je pak 5/28.
b) N=9, M=3, n=3, x=2.
c) N=9, M=3, n=3, x=3.
Offline
#2 12. 10. 2019 15:02 — Editoval Ferdish (12. 10. 2019 15:07)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Pravděpodobnost - kuličky
Všetky ťahy sú navzájom nezávislé javy - pp výsledného javu je súčin pp-í jednotlivých nezávislých javov. Na to stačia teória a úvahy pp a štatistiky zo SŠ...
Offline
#3 12. 10. 2019 15:15
Re: Pravděpodobnost - kuličky
↑ Ferdish: Tahá se bez vracení, takže ty tahy nejsou nezávislé.
Offline
#5 12. 10. 2019 16:48
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Pravděpodobnost - kuličky
↑ Ferdish:
Mohu se tedy zeptat, jak by to a) mělo vypadat? Pak tedy jen 1/3 na třetí?
Offline
#6 12. 10. 2019 20:22
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Pravděpodobnost - kuličky
↑ xstudentíkx:
Trochu som sa unáhlil v tom, že to bude súčin pp-í všetkých troch ťahov...no pre prvý ťah sa nevzťahuje žiadna obmedzujúca podmienka. Ako prvú môžeme vytiahnuť guľôčku akejkoľvek farby. Nemá teda zmysel uvažovať o pp prvého ťahu. Jeho výsledok však ovplyvní pp ostatných ťahov.
Analogickými úvahami možno vyriešiť aj úlohy b) a c).
Offline
#7 12. 10. 2019 22:04
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Pravděpodobnost - kuličky
↑ Ferdish:
Skvělé, moc děkuji, toto mi dává smysl :)
Zároveň by se to tedy dalo i v kombinačních čísel kde v čitateli budu mít třikrát výběr 1 kuličky ze 3 a dole celkový výběr a to 3 kuličky z 9. Dojdu k úplně stejnému výsledku.
Mám už to celé a dokonce dvěma způsoby všechno, moc díky!
Offline
#8 12. 10. 2019 22:21
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Pravděpodobnost - kuličky
↑ xstudentíkx:
:-)
Veľa zdaru!
Offline
 , lebo 6 prípadov z 8 možných je pre nás priaznivých. Zlomok sa dá ešte skrátiť na základný tvar
, lebo 6 prípadov z 8 možných je pre nás priaznivých. Zlomok sa dá ešte skrátiť na základný tvar 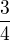
 , lebo 3 prípady zo 7 možných sú pre nás priaznivé.
, lebo 3 prípady zo 7 možných sú pre nás priaznivé.