Matematické Fórum

Maca · 12. 09. 2009 17:17

Můžete mi, prosím, zkontrolovat správnost postupu řešení tohoto příkladu:
Zapište jako lineární kombinaci vždy všech 4 vektorů a1=(0,0,0,1) a2=(0,0,2,0) a3=(0,3,0,0) a4=(4,0,0,0) vektor x=(8,9,4,1).
x=a1*r + a2*s + a3*t + a4*z x=.....
8=0*r + 0*s + 0*t+ 4*z 9=0kr + 0ks + 3kt + 0kz 4=0kr + 2ks + 0kt + 0kz 1=1kr + 0ks + 0kt + 0kz
2=z 3=t 2=z 1=k

A jak dál? Ještě někam dosadit, aby se zjistila rovnost? Nebo jsem mohla dosadit už do té poslední rovnice? To asi ne.

Maca · 12. 09. 2009 17:18

↑ Maca:
Omlouvám se, ta malá k měla být *, jako násobení

LukasM · 12. 09. 2009 19:16

↑ Maca:
Myslíš to asi dobře, ale ten poslední řádek je opsanej šíleným způsobem. Dvakrát tam máš že z=2, neznámá s není vyjádřená vůbec a místo neznámé r je vyjádřené jakési k, které se v původní rovnici vůbec nevyskytuje.
Nicméně, pokud ten závěr měl být, že z=2, t=3, s=2 a r=1, tak já s tím souhlasím, a nechápu co chceš dělat dál. Prostě x=1*a1 + 2*a2 + 3*a3 + 2*a4. Pokud si to chceš ověřit, stačí si spočítat tu pravou stranu a vyjde ti levá. Nebo v čem je přesně problém?

Maca · 12. 09. 2009 20:58

Děkuji a ještě jednou se omlouvám - hučely do mě děti a toto je výsledek - stydím se.
Takže zakončení : 8 + 9 + 4 + 1 = 1*1 + 2*2 + 3*3 + 2*4
22=22
je postačující?
Moc děkujji.

LukasM · 12. 09. 2009 21:12

↑ Maca:
Ne, tohle je nesmysl. Souřadnice vektorů nemůžeme začít jen tak sčítat. Postačující zakončení je 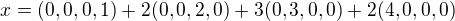$x=(0,0,0,1)+2(0,0,2,0)+3(0,3,0,0)+2(4,0,0,0)$ . Nalézt ta čtyři čísla je smysl příkladu.

Ověření že je to dobře by proběhlo následujícím způsobem - vezmeme pravou stranu té rovnosti a vypočítáme kolik to je. Mělo by vyjít (8,9,4,1). Přesvědčme se o tom: 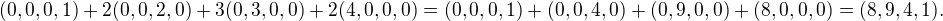$(0,0,0,1)+2(0,0,2,0)+3(0,3,0,0)+2(4,0,0,0) = (0,0,0,1)+(0,0,4,0)+(0,9,0,0)+(8,0,0,0)=(8,9,4,1).$ Při tomhle výpočtu musí nicméně vektory zůstat vektory. Proto je jako vektory násobím (všechny souřadnice daným číslem) a stejně tak sčítám (příslušné souřadnice spolu).

Je to trochu jasnější?

Maca · 12. 09. 2009 21:51

Děkuji za polopatické vysvětlení - přesně to potřebuji ! :)

Matematické Fórum

#1 12. 09. 2009 17:17

Lineární kombinace vektorů

#2 12. 09. 2009 17:18

Re: Lineární kombinace vektorů

#3 12. 09. 2009 19:16

Re: Lineární kombinace vektorů

#4 12. 09. 2009 20:58

Re: Lineární kombinace vektorů

#5 12. 09. 2009 21:12

Re: Lineární kombinace vektorů

#6 12. 09. 2009 21:51

Re: Lineární kombinace vektorů

Zápatí