Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 12. 2019 15:15 — Editoval Roscelinius (26. 12. 2019 15:23)
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Lineární transformace v duálním prostoru
Dobrý den,
Prosím o pomoc.
Lineární transformace  zadana v bázi
zadana v bázi 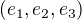 maticí
maticí 
Mám určit bázi v tenzorovem prostoru  a v této bázi zapsat indukované zobrazeni
a v této bázi zapsat indukované zobrazeni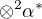 .
.
Jestli to chápu správně tak matice transformace v duální bázi je inverzní. Onen prostor je prostor tenzoroveho součinu duálních prostoru?
Děkuji za jakoukoliv pomoc.
Petr
Offline
#2 26. 12. 2019 17:22
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Lineární transformace v duálním prostoru
Je ona hledaná báze jednoduše: .
.
Nemůžu ale vyspekulovat, jak přepsat to zobrazeni. Napadá mě jen tenzorovy součin dvou inverzních matic z té původní, to se mi ale moc nezdá.
Děkuji za reakce.
Offline