Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 09. 2009 21:48
Velikost vektoru
Chtěla bych poprosit o kontrolu postupu řešení následujícího příkladu:
Určete velikost vektoru x, platí-li 2(a+x) + 3(b+x)= 6x + c , kde a=(1,2,3,4), b=(0,1,2,3), c=(2,7,12,19).
2(1+x) + 3(0+x)= 6x + 2 2(2+x) + 3(1+x) =6x + 7 2(3+x) + 3(2 + x)=6x + 12 2(4 + x) + 3(3 + x)=6x + 19
2 + 2x + 0 + 3x = 6x + 2 4 + 2x + 3 + 3x =6x + 7 6 + 2x + 6 + 3x =6x + 12 8 + 2x + 9 + 3x =6x + 19
2 + 5x = 6x + 2 7 + 5x =6x +7 12 + 5 x =6x + 12 17 + 5x =6x + 19
0 = x 0 = x 0 = x -2 = x
Je postup správně? Děkuji.
Offline
#2 12. 09. 2009 22:00
Re: Velikost vektoru
↑ Maca:
Postup je v zásadě správně, akorát by to příště chtělo líp zapsat. Konkrétně mi jde o to, že na konci příkladu je čtyřikrát x=(něco), což nic moc neříká. To se x rovná zároveň nule i mínus dvojce? Chápu samozřejmě, že to měly být složky toho vektoru x, ale pak je potřeba je označit každou jinak a napsat co je co. Třeba se dá zapsat: x=(0,0,0,-2), to je asi nejhezčí zápis výsledku.
V zadání se ptají na velikost toho vektoru, takže asi chtějí slyšet prostě číslo 2.
Poznámka na okraj: zadání ale není úplně korektní, protože když se ptá na velikost, mělo by taky definovat skalární součin (od něj se odvíjí velikost) - a tady je právě namístě otázka, jak hluboko do algebry je potřeba se nořit, viz. vedlejší vlákno.
Offline
#4 12. 09. 2009 23:53
Re: Velikost vektoru
↑ Maca:
Vzhledem k tomu co padlo vedle v tématu lineární prostor tady není třeba dopodrobna definovat velikost vektoru. Pro tvoje účely by mělo stačit následující. Zkus si představit prostor dvojic čísel - podobně jako ty trojice se to dá brát jako prostor šipek vycházejících z počátku, ale tentokrát budou všechny v jedné rovině. Velikostí vektoru se nemyslí nic jiného, než délka takové šipky. Z Pythagorovy věty snadno vyplyne, že šipka odpovídající vektoru (2,1) má délku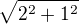 
.
Stejným způsobem se vypočítá velikost jakékoli n-tice: u trojice (3,4,5) je to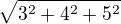 
apod. U naší čtveřice (0,0,0,-2) je to tedy 
.
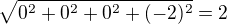Opět tohle není obecně pravda, ale mělo by to stačit.
Offline
#5 13. 09. 2009 07:25
Re: Velikost vektoru
Díky, přesně jste trefil tip vysvětlování pro mou osobu.
Uznávám, že moje otázky zní občas jak z Marsu.. Ale na to, že jsem všechny termíny a vzorce viděla před 14 dny poprvé v životě (máme to bez výkladu), je malý zázrak, že se dostanu sama alespoň do poloviny příkladu. Budu moc vděčná, když se mnou vydržíte ten půlrok. Budu se snažit nastudovat co nejvíc a prudit co nejmíň :)
Offline