Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 01. 2020 21:53
Metoda konečných prvků
Dostal jsem na stará kolena bláznivý nápad si naprogramovat nějaký výpočet parciální rovnice metodou konečných prvků. Akorát si už moc nepamatuji, jak se to dělá (po pravdě jsem to nejspíš nikdy pořádně nevěděl).
Nemusí to být nic složitého, třeba Laplaceova rovnice, pro začátek klidně i v 1D, ale chtěl bych zkusit aspoň 2D (to se dá ještě tak nějak rozumě vykreslit do grafu).
Vzpomínám si, že ten "konečný prvek" byl (v 1D případě) taková stříška o základně 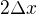 a nějaké výšce - a že řešení bylo aproximováno součtem těchto stříšek (o různé výšce) navzájem posunutých o
a nějaké výšce - a že řešení bylo aproximováno součtem těchto stříšek (o různé výšce) navzájem posunutých o 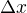 .
.
A pak byla nějaká metoda, jak pro "výšky stříšek" - ty koeficienty prvků napsat nějaku soustavu lineárních rovnic. To si ale právě už nepamatuji ... tuším že metod bylo víc a jedna z nich se jmenovala Galerkinova metoda, víc ale už nevím.
Neporadil by mi někdo ?
Primárně mi jde o to si to zkusit naprogramovat, ale když už to budu dělat, tak bych to taky rád pochopil...
Offline
#2 02. 04. 2020 22:32
Re: Metoda konečných prvků
Galerkinova metoda znamena obecne to, ze reseni sve rovnice hledas pouze v nejakem konecne dimenzionalnim podprostoru a pote v nejakem smyslu provedes limitu, kde se dimenze blizi nekonecnu. Napr., pokud budu vedet, ze moje reseni patri do nejakeho separabilniho prostoru a podari-li se mi zvolit vhodny skalarni soucin, pak muzu podprostory konstruovat jako linearni obal prvnich n prvku prislusne huste podmnoziny. Timto vlastne diskretizuji prostorovou promennou a tudiz misto PDR dostavam jen system algebraickych rovnic, nebo obycejnych dif. rovnic v evolucnich problemech. To bych rekl, ze je hlavni myslenka a muzes si ji snadno overit tak, ze vezmes svou oblibenou PDR a za reseni dosadis ,
,
kde vektory 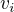 tvori tu bazi celeho prostoru a
tvori tu bazi celeho prostoru a 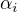 jsou hledane koeficienty.
jsou hledane koeficienty.
Na metodu konecnych prvku se pak da pohlizet jako na urcitou specifikaci Galerkinovy metody, ktera je konstruovana tak, aby se dala dobre naprogramovat. Potrebujes hlavne definovat 2 veci: Jak bude vypadat tvoje vypocetni sit (tj. jak rozkouskujes domenu) a pak jak zvolis bazove funkce. To jsou prave ty strisky, ktere dostanes pokud zvolis po castech linearni aproximaci a reknes si, ze v uzlu i bude bazova funkce j nabyvat 1 prave kdyz i=j. To formalni prevedeni PDR na algebraickou soustavu je pak dost podobny jako v obecny Galerkinove metode, akorat tech nenulovych clenu z tech skalarnich soucinu bude malinko vic (kdykoliv se potkaji supporty tech bazovejch funkci- coz obvykle vede na nejakou tridiagonalni matici).
Kdybys tapal, napis nejakou konkretni rovnici a domenu, kde by te to zajimalo resit..
Offline
#3 03. 04. 2020 16:53
Re: Metoda konečných prvků
Myslel jsem nějakou jednoduchou rovnici, třeba Laplaceovu ve 2D, 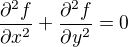
třeba dva čterce, kus od sebe, každý z nich na jiném potenciálu ... a spočítat rozložení potenciálu kolem nich... a nebo jakékoliv jiné okrajové podmínky...
Offline
