Matematické Fórum

Arabidopsis · 11. 02. 2020 13:42

Ahoj, potřebovala bych si ověřit, že postupuji správně

1) Mějme soustavu rovností
$y = x^{2}e^{z} + b - 3$
$a = e^{z}$
$c = b - 3$

Vypište všechny dvojice proměnných, které jsou v lineárním stavu.

Dosazením získám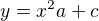
$y = x^{2}a + c$

Lineární vztah obecně vnímám jako: f(x):y = ax + b, zobrazením je přímka.
Proto: v zadané soustavě rovnic vidím dvojice v lineárním vztahu ya, yc, yb a bc.

2) Mějme veličinu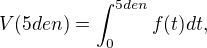
$V(5 den) = \int_{0}^{5 den}f(t)dt,$
kde t jsou dny a f(t) = at^{2} rychlost růstu rostliny.
Jaké jsou jednotky veličin V, a?
Logicky očekávám, že V je délka rostliny (např. v cm), t jsou dny, a = cm/den (jednotkově to sedí).
Pokud je a = 3, V (5 den) se bude rovnat 125 cm.

3) Mějme aproximativní závislost plochy listů O na vlhkosti substrátu V a koncentraci fosforu P.
$O = 3V^{\frac{1}{3}} + 300 P$
Jakou naměříme rychlost změny listové plochy se změnou koncentrace dusíku v krajině, kde platí V = 6400 P^{3}?
Dosadím do vzorce a vyjde mi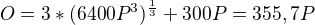 $O = 3*(6400P^{3})^{\frac{1}3{}} + 300 P = 355,7 P$
Nevím, co máš ještě udělat, abych získala tu "rychlost změny", udělat derivaci? Dosadit libovolnou hodnotu za P a O do obou vztahů a porovnat? Nebo bych rovnou napsala delta O = vztah1/vztah2.

Moc děkuji!

jelena · 14. 02. 2020 23:15

Zdravím,
pokud je ještě aktuální:

a) "lineární stav" se rozumí "lineární vztah"? Potom bych uvažovala také inverzní funkce, co vzniknou, tedy v obecném zápisu pokud je lineární vztah y=f(x), potom je také lineární i inverzní funkce a x=g(y)? Je to tak?

b) pokud je $f(t) = at^{2}$ rychlost růstu, a čas $t$ je ve dnech, růst v cm, potom rychlost růstu je v cm/den a odvodím rozměrnost pro $a$ ze vztahu, $a=\frac{f(t)}{t^2}$ , což mi vychází jinak, než navrhuješ. Zkontrolovat lze také použitím integrálu, dle zadání. Ohledně vztahu s časem se mi to jeví celkem jednoznačně, ale z čeho víme, že růst bereme jen v jednom směru (tedy cm, ale ne v prostoru?), to je jen na upřesnění, děkuji.

c)

rychlost změny listové plochy se změnou koncentrace dusíku v krajině

máme v zadání závislost na koncentraci dusíku? je to jen překlep, nebo pointa úlohy? Děkuji.

Matematické Fórum

#1 11. 02. 2020 13:42

Lineární vztah dvou proměnných + slovní úloha na integrál ke kontrole

#2 14. 02. 2020 12:21 Příspěvek uživatele Rumburak byl skryt uživatelem Rumburak.

#3 14. 02. 2020 23:15

Re: Lineární vztah dvou proměnných + slovní úloha na integrál ke kontrole

Zápatí