Matematické Fórum

thorne · 08. 03. 2020 09:30

Ahoj,

je tohle správně provedený důkaz? (na netu jsem to nenašel)
Doteď jsem řešil jen příklady, které nebyl problém zapsat L=součet(n)+následující člen
P=součet(n+1)
Tady ale nevím no.

$a^{n}-b^n=(a-b)\Sigma a^{k}b^{n-k-1}$
Suma od k=0 do n-1

Autor skryl část textu. Zobrazit/skrýt!

vanok · 08. 03. 2020 11:24

Ahoj ↑ thorne:,
Princip je dobry. No napis ten dokaz uplne podrobne. Vies to urobit?

krakonoš

↑ thorne:
Ahoj u L=.... máš znaménko plus místo mínus. Uvádíš zde co máme dokázat, ale ne postup jak využít ind předpoklad. Já osobně bych ti doporučila při důkazu využít úpravy
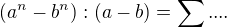$(a^{n+1}-b^{n+1}):(a-b)=a[(a^{n}-b^{n})+b^{n}-\frac{b}{a}b^{n}]:(a-b)$ , zde už můžeš využít ind předpoklad, že $(a^{n}-b^{n}):(a-b)=\sum_{}^{}....$ . vyjít z tohoto tvaru indukčního předpokladu je nejjednodušší, protože při důkazu můžeš použít normální úpravu výrazů, jak uvádím výše. Možná ale máš jinou myšlenku, případně ji můžeš uvést

thorne · 08. 03. 2020 13:35

Díky, určitě to vyzkouším.
Já žádnou myšlenku právě neměl no.

vanok · 08. 03. 2020 19:00

↑ thorne:,
Poznamka.
Iste tu vlasnost, dokazes dokonale indukciou dokazat.

No ale existuju aj ine dokazy tejto vlasnosti.
Napr. Tato vlasnost sa da dokazat vdaka suctu vhodnej geometrickej rady.
Ina moznost: je znama veta ( ktora sa pouziva aj pri dokaze Viète-ovych vlasnosti) faktorizacie polynomov vdaka ich korenom.

jarrro · 09. 03. 2020 10:27

$a^{n+1}-b^{n+1}=a$a^n-b^n$+$a-b$b^n$

Autor skryl část textu. Zobrazit/skrýt!

thorne · 13. 03. 2020 20:13 — Editoval thorne (13. 03. 2020 20:14)

mám to, díky za vysvětlení, možnosti a nakonec i postup :)

Matematické Fórum

#1 08. 03. 2020 09:30

Mat. indukce

#2 08. 03. 2020 11:24

Re: Mat. indukce

#3 08. 03. 2020 11:53 — Editoval krakonoš (08. 03. 2020 12:10)

Re: Mat. indukce

#4 08. 03. 2020 13:35

Re: Mat. indukce

#5 08. 03. 2020 19:00

Re: Mat. indukce

#6 09. 03. 2020 10:27

Re: Mat. indukce

#7 13. 03. 2020 20:13 — Editoval thorne (13. 03. 2020 20:14)

Re: Mat. indukce

Zápatí