Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 03. 2020 08:12
- stuart clark

- Příspěvky: 1015
- Reputace: 7
product of definite integration
If ![kopírovat do textarea $f:[0,1]\rightarrow (0,\infty)$](/mathtex/5c/5c142183ea3359f94450893ed04f67a2.gif) is a continuous function such that
is a continuous function such that 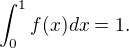
Then maximum value of ![kopírovat do textarea $\displaystyle \bigg(\int^{1}_{0}\sqrt[3]{f(x)}dx\bigg)\bigg(\int^{1}_{0}\sqrt[5]{f(x)}dx\bigg)\bigg(\int^{1}_{0}\sqrt[7]{f(x)}dx\bigg)$](/mathtex/bd/bdf6f819eb09f5bf10a45ab1b45fc290.gif)
Offline
#2 16. 03. 2020 11:31
Re: product of definite integration
Offline
#3 17. 03. 2020 10:01
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: product of definite integration
Thanks ↑ laszky:
i solved like this way![kopírovat do textarea $\bigg(\int^{1}_{0}\sqrt[3]{f(x)}dx\bigg)^3\leq \int^{1}_{0}f(x)dx$](/mathtex/46/469bba97d90aa01d18854abe05b5d516.gif)
![kopírovat do textarea $\bigg(\int^{1}_{0}\sqrt[5]{f(x)}dx\bigg)^5\leq \int^{1}_{0}f(x)dx$](/mathtex/35/35b5407d30417f45fc6beb68d580f4c3.gif)
![kopírovat do textarea $\bigg(\int^{1}_{0}\sqrt[7]{f(x)}dx\bigg)^7\leq \int^{1}_{0}f(x)dx$](/mathtex/77/77c34fb1a4b66488c5eb38a2a200463e.gif)
So ![kopírovat do textarea $\int^{1}_{0}\sqrt[3]{f(x)}dx\cdot \int^{1}_{0}\sqrt[5]{f(x)}dx\cdot \int^{1}_{0}\sqrt[7]{f(x)}dx\leq \bigg(\int^{1}_{0}f(x)\bigg)^{\frac{1}{3}}\bigg(\int^{1}_{0}f(x)\bigg)^{\frac{1}{5}}\bigg(\int^{1}_{0}f(x)\bigg)^{\frac{1}{7}}=1$](/mathtex/46/46bcbff19f23a69f64167b8cd8a3f888.gif) $
$
Offline
 and
and 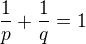 ,
,  it follows that
it follows that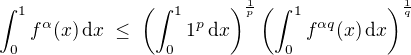
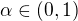 ,
, 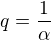 and
and  we obtain
we obtain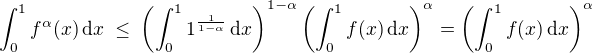
![kopírovat do textarea $\displaystyle \bigg(\int^{1}_{0}\sqrt[3]{f(x)}dx\bigg)\bigg(\int^{1}_{0}\sqrt[5]{f(x)}dx\bigg)\bigg(\int^{1}_{0}\sqrt[7]{f(x)}dx\bigg) \leq \left(\int_0^1 f(x)\,\mathrm{d}x\right)^{\frac{1}{3}+\frac{1}{5}+\frac{1}{7}} = \left(\int_0^1 f(x)\,\mathrm{d}x\right)^{\frac{71}{105}} = 1^{\frac{71}{105}} = 1$](/mathtex/49/490086f7f973cb78eda37e5f3fa1837f.gif)
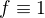 .
.