Matematické Fórum

surovec · 23. 03. 2020 07:39

Máme dostupné údaje o počtu nově nakažených v ČR v jednotlivých dnech (třeba tady). Z nich máme epidemickou křivku. Tato křivka (pokud se nepletu) je aproximována Gaussovou křivkou. A teďkon bych chtěl z těch údajů zjistit, kdy bude počet denních případů kulminovat a jaký bude maximální denní počet nakažených - pojďme to společně spočítat a později porovnat s reálným vývojem! (Jsem si vědom, že současné počty jsou ovlivněny také počtem testovaných, měnící se motivací jít na test, použitým testem atd., ale jde o odhad, který můžeme každý den zpřesňovat.)
Můj návrh výpočtu:
1) Současné údaje, které jsou dost nevyrovnané, proložit vhodnou regresní křivkou. A tady je největší problém, jakou? Exponenciální? Mocninou? Jinou?
2) Z vypočítané regresní křivky si spočítat tři body (to by mi mělo v dalším kroku stačit k určení té Gaussovky). Ale jaké body? Já navrhuji v 1/4, v 1/2 a ve 3/4 intervalu (dosavadního časového úseku).
3) Teď už jen dosadit do Gaussovy funkce a určit koeficienty 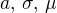$a,\,\sigma,\,\mu$ (samozřejmě pomocí matematického softwaru), to už je triviální.
Jsou to nesmysly, nebo je to správný postup?

check_drummer · 23. 03. 2020 12:12

Ahoj,
1) Jak víš, že jde o Gaussovu křivku?
2) Podle mě ta křivka může být jiná, když je karanténa a když je volný pohyb lidí, dokonce může jít, myslím si, i o jiný typ křivky
3) Proč v bodě 1) rovnou nevolíš Gausovu křivku? (Pokud tedy ta je ta správná.)

surovec · 23. 03. 2020 12:23

↑ check_drummer:
1) Že je Gaussova vyvozuji z grafů v epidemiologických textech. Je pravda, že explicitně řečený to tam není.
2) Samozřejmě, že ji mohou ovlivnit další faktory, vždyť to píšu i v zadání. Ale pokud jde o predikci dalšího vývoje, tak je to prostě nejlepší odhad, s jakým můžeme pracovat. Všichni přece ví, že statistika není opravdová matematika :-)
3) Nevolím ji, protože ty údaje samozřejmě tu křivku přesně nekopírují. Když budeš v reálu měřit něco s normálním rozdělením (třeba tvrdost nějakého materiálu, IQ atd.), tak ty údaje "nikdy" nebudou přesně kopírovat tu křivku. Jen se to k ní bude s rostoucím počtem údajů limitně blížit. A v České republice máme jen 22 údajů (od 1. března).

check_drummer · 23. 03. 2020 12:29

↑ surovec:
A proč to nebrat jako exponeniální křivku? Než se začnou lidi uzdravovat, tak by to možná šlo ne?
Akorát základ té exponenciely se hodně změnil po vyhlášení karantény...
A nedalo by se to modelovat na základě dat i v jiných státech? Kdybychom předpokládali podobný vývoj.

surovec · 23. 03. 2020 12:55

↑ check_drummer:
1) No ona to obyčejná exponenciela být nemůže, páč se snižuje množství lidí, kteří ještě mohou být infikováni. Ale ze začátku to samozřejmě podobné je. Tím bychom možná odpověděli na první otázku - jako regresní křivku volit exponenciální regresi.

Stýv · 23. 03. 2020 13:35

surovec napsal(a):
Všichni přece ví, že statistika není opravdová matematika :-)

A pak vymýšlejí takový nesmyslný způsoby prokládání dat, jako ty teď. ;-)

surovec · 23. 03. 2020 14:02

↑ Stýv:
To já můžu. Já totiž nejsem opravdový matematik :-)

Matematické Fórum

#1 23. 03. 2020 07:39

Koronavirus - reálná matematika - inspirace laszkym

#2 23. 03. 2020 12:12

Re: Koronavirus - reálná matematika - inspirace laszkym

#3 23. 03. 2020 12:23

Re: Koronavirus - reálná matematika - inspirace laszkym

#4 23. 03. 2020 12:29

Re: Koronavirus - reálná matematika - inspirace laszkym

#5 23. 03. 2020 12:55

Re: Koronavirus - reálná matematika - inspirace laszkym

#6 23. 03. 2020 13:35

Re: Koronavirus - reálná matematika - inspirace laszkym

surovec napsal(a):

#7 23. 03. 2020 14:02

Re: Koronavirus - reálná matematika - inspirace laszkym

Zápatí