Matematické Fórum

bramburka · 03. 04. 2020 11:30

//forum.matweb.cz/upload3/img/2020-04/04174_fyzika%2Bp%25C5%2599.%25C4%258D.5.jpg

Krásný dobrý den,
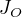chci řešit tento příklad a nevím, jestli nejdu úplně špatným směrem. Chtěla bych to počítat přes Steinerovu větu, ale docela mě mate, že to prochází normálně těžištěm a středem objektu. 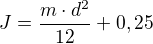Bylo by to tedy jako $J=J_{o}+m\cdot a^{2}$ kde za $J_{O}$ bych dosadila to ze zadání, s tím, že pro to ale nevím kokrétní hodnoty a za $m$ bych dosadila zadanou hmotnost čtverce 1kg a za $a$ bych dosadila polovinu zadané strany tedy $(0,5)^{2}$ Takže by to vycházelo jako $J=\frac{m\cdot d^{2}}{12}+ 0,25$ A v tomto okamžiku už s tím nemám moc víc co udělat ne? Budu vděčná za jakoukoliv pomoc :)

LukasM · 03. 04. 2020 11:41 — Editoval LukasM (03. 04. 2020 11:45)

↑ bramburka:
Já asi nechápu co, je to "homogenní drátěný čtverec". Ze slova drátěný bych chápal, že jsou to čtyři tyče v rozích spojené a uvnitř nic. Ze slova homogenní bych chápal. že je to plošný útvar. To je samozřejmě zásadní pro volbu postupu.

Kdyby to byly čtyři ryče v rozích spojené, mělo by jít z hmotnosti čtverce určit hmotnost tyče, spočítat její moment setrvačnosti, Steinerovou větou ho přepočítat vůči vnější ose a vynásobit čtyřmi. Tvůj postup moc nechápu, ale přijde mi, že motá dohromady parametry tyče a čtverce.

Ale protože autor úlohy si nedal ani tolik práce, aby stranu a hmotnost označil jinými písmeny, tak je asi možné všechno.

bramburka · 03. 04. 2020 12:19

Takže pokud bych to počítala jako drátěný čtverec( jako 4 tyče spojené v rozích) bude mi vůbec k něčemu informace o té tyči nad tím? Jak s tím souvisí? Když by byl útvar uprostřed prázdný..

zabijal10

↑ LukasM:
Vypočítal jsem moment setrvačnosti jedné tyče (mám stejnou úlohu, pouze s jinými údaji) :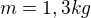
$m = 1,3 kg$ , délka strany $a = 1,5m$ : $J_{0}= \frac{1}{12}\cdot \frac{1,3}{4}\cdot 0,75^{2}=\frac{32}{2560}kg\cdot m^{2}$
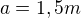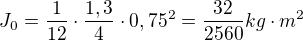
Mohl byste prosím upřesnit, co myslíte "přepočítáním vůči vnější ose" ? Protože pokud osa otáčení prochází těžištěm, bude vzdálenost od těžiště 0 a tím pádem po přepočítání dostanu stejný výsledek. Děkuji

LukasM · 04. 04. 2020 08:49

bramburka napsal(a):
bude mi vůbec k něčemu informace o té tyči nad tím? Jak s tím souvisí?

Samozřejmě, že bude. Souvisí to s tím tak, že moment setrvačnosti je aditivní, takže když si ze čtverce odmyslím tři tyče a zůstane mi jedna, mohu snadno spočítat čtvrtinu výsledku. Jediná otázka zní, kolik tento moment setrvačnosti je, protože taková tyč už nerotuje kolem té osy, vůči které ten moment známe. A tady právě pomůže Steinerova věta.

zabijal10 napsal(a):
$J_{0}= \frac{1}{12}\cdot \frac{1,3}{4}\cdot 0,75^{2}=\frac{32}{2560}kg\cdot m^{2}$

Ne, bohužel ani dosadit do vzorce se ti nepodařilo. Délka tyče je 1.5 m, ne 75 cm. Naprosto zbytečně dosazuješ čísla - bude lepší se co nejdéle držet písmenek. Nakonec řešíš stejný problém, jako kolegyně výše, není třeba to tu komplikovat.

Mohl byste prosím upřesnit, co myslíte "přepočítáním vůči vnější ose" ?

Tím myslím to, že když je tyč součástí čtverce, tak už nerotuje kolem svého těžiště. Zkoušeli jste si to alespoň nakreslit?

Matematické Fórum

#1 03. 04. 2020 11:30

moment setrvačnosti drátěného čtverce pomoc

#2 03. 04. 2020 11:41 — Editoval LukasM (03. 04. 2020 11:45)

Re: moment setrvačnosti drátěného čtverce pomoc

#3 03. 04. 2020 12:19

Re: moment setrvačnosti drátěného čtverce pomoc

#4 03. 04. 2020 16:14 — Editoval zabijal10 (03. 04. 2020 16:16)

Re: moment setrvačnosti drátěného čtverce pomoc

#5 04. 04. 2020 08:49

Re: moment setrvačnosti drátěného čtverce pomoc

bramburka napsal(a):

zabijal10 napsal(a):

Zápatí