Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Ty nejzajímavější úlohy z teorie čísel
- » $x^4 +y^4=z^4$ (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 04. 2020 10:50 — Editoval vanok (07. 04. 2020 14:08)
$x^4 +y^4=z^4$
Pozdravujem,
Je skor jednoduche dokazat, ze rovnica 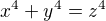 nema riesenie v
nema riesenie v  . (a)
. (a)
A tiez iste viete, ze tato rovnica
nie je riesitelna 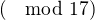 (b)
(b)
ale je riesitelna 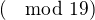 (c).
(c).
Viete dokazat (a), (b) a (c)?
A ako je to vseobecnejsie?
ÉDIT. Ide pochopitelne o nenulove riesnia ako poznamenal kolega check_drummer.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
- (téma jako vyřešené označil(a) vanok)
#2 07. 04. 2020 12:17
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: $x^4 +y^4=z^4$
"Máte úhel beta." "No to nemám."
Offline
#3 07. 04. 2020 14:29 — Editoval vanok (07. 04. 2020 14:31)
Re: $x^4 +y^4=z^4$
Ahoj ↑ check_drummer:,
To si dobre popisal situaciu v pripadoch (a), (b), (c).
No ale posledna (tazka) otazka je naozaj zaujimava.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Ty nejzajímavější úlohy z teorie čísel
- » $x^4 +y^4=z^4$ (TOTO TÉMA JE VYŘEŠENÉ)

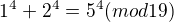
 . Ale asi nás zajímají jen čísla nedělitelná 17. Pak lze ukázat, že jejich čtvrté mocniny dávají zbytek po dělení 17 jen 1,4,16 nebo 13 a součtem dvou z nich nedostaneme třetí. Je to také návod pro obecný postup, ale je nutné ty zbytky vygenerovat a prozkoumat, možná existuje něco elegantnějšího.
. Ale asi nás zajímají jen čísla nedělitelná 17. Pak lze ukázat, že jejich čtvrté mocniny dávají zbytek po dělení 17 jen 1,4,16 nebo 13 a součtem dvou z nich nedostaneme třetí. Je to také návod pro obecný postup, ale je nutné ty zbytky vygenerovat a prozkoumat, možná existuje něco elegantnějšího.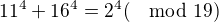 .
. 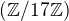 je radu 16 a tak pre kazdy jej prvok
je radu 16 a tak pre kazdy jej prvok  mame
mame 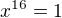 ...
...