Matematické Fórum

statistika_je_naj

Ahojte, mam takyto priklad. Mam hod dvoma kockami naraz
X - je nahodna premenna, ktora reprezentuje cisla mensie alebo rovne 3
Y - je nahodna premenna, ktora reprezentuje cisla vacsie ako 3
Mam urcit kovarianciu cov(XY)
Postupoval som takto:

Hody su
11 21 31 41 51 61
12 22 32 42 52 62
13 23 33 43 53 63
14 24 34 44 54 64
15 25 35 45 55 65
16 26 36 46 56 66

Dostal som:
x P(x)
0 9/36
1 27/36

a
y P(y)
0 9/36
1 27/36

potom
dostavam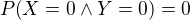

$P{$X=0\wedge Y=0$}=0$
$P{$X=0\wedge Y=1$}=9/36$
$P{$X=1\wedge Y=0$}=9/36$
$P{$X=1\wedge Y=1$}=18/36$

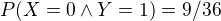
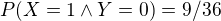
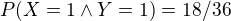
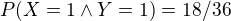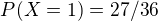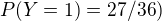kedze $P{$X=1\wedge Y=1$}=18/36$ ale $P(X=1)=27/36$ , $P(Y=1)=27/36)$ tak nie su zavisle.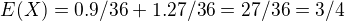
$E(X)=0.9/36+1.27/36=27/36=3/4$
$E(Y)=0.9/36+1.27/36=27/36=3/4$

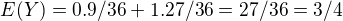
a podla vztahu
$E{$XY$}=\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}{x_iy_jP{$X=x_i\wedge Y=y_j$}}$

som dostal: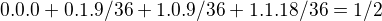

$0.0.0+0.1.9/36+1.0.9/36+1.1.18/36=1/2$
teda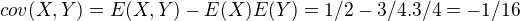
$cov(X,Y)=E(X,Y)-E(X)E(Y)=1/2-3/4.3/4=-1/16$

mam to dobre? Ak nie tak prosim vas kde je chyba?

Matematické Fórum

#1 07. 04. 2020 19:34 — Editoval statistika_je_naj (07. 04. 2020 19:35)

kovariancia 2

Zápatí