Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 04. 2020 18:34
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Dělení obdélníka
Ahoj, obdélník je rozdělen na obdélníkové části, jejichž alespoň jedna strana je vždy celé číslo. Dokažte, že pak alespoň jedna strana celého obdélníka je celočíselná.
"Máte úhel beta." "No to nemám."
Offline
#3 11. 04. 2020 18:54
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Dělení obdélníka
↑ MichalAld:
Ahoj, řekl bych že ano. Máš protipříklad s nekonečným počtem, kdy to neplatí? Pokud ne, tak zatím ponechme i možnost nekončného počtu obdélníků.
"Máte úhel beta." "No to nemám."
Offline
#4 13. 04. 2020 08:53 — Editoval vanok (13. 04. 2020 08:54)
Re: Dělení obdélníka
Pozdravujem ↑ check_drummer:,
Tvoj problem sa trochu podoba na
Ak dany obdlznik stran 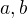 je rozdeleny na stvorce stran
je rozdeleny na stvorce stran 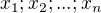 tak
tak 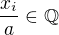 a
a 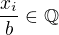 pre
pre 
(Podla Praslova v jeho knihe tykajucej sa linearnej algebry ).
A tvoje cvicenie je akeho povodu ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 13. 04. 2020 10:21
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Dělení obdélníka
Ahoj, já jsem to kdysi našel někde na internetu a teď jsem si na to vzpomněl. Ale myslím, že ten důkaz lineární algebru nepužíval.
"Máte úhel beta." "No to nemám."
Offline
