Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 04. 2020 18:10
- nononsense

- Příspěvky: 110
- Reputace: 1
Logaritmická nerovnice
Ahoj, dneska poslední dotaz a doufám, že jich už mnoho nepřibude.
Mám takto zadanou nerovnici: 
vyšlo mi 
Jak to, že je výsledné řešení 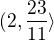
mně totiž vyšlo 
podmínky mám tyto: x<2, x>3
díky moc!
Offline
- (téma jako vyřešené označil(a) nononsense)
#2 16. 04. 2020 18:35 — Editoval Rumburak (16. 04. 2020 18:44)
Re: Logaritmická nerovnice
↑ nononsense:
Ahoj.
Předpokládejme, že symbolem 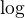 je míněna logaritmická funkce o základu 10, jak je obvyklé.
je míněna logaritmická funkce o základu 10, jak je obvyklé.
Je potřeba si uvědomit tři věci:
1. Definičním oborem logaritmické funkce je množina všech kladných čísel - odtud podmínka na zlomek ve vztahu
(1)  .
.
2. Každá logaritmocká funkce o základu větším než 1 je rostoucí.
3. Pro každé reálné  platí
platí 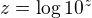 .
.
Offline
#3 16. 04. 2020 20:10
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
tak teď jsem trochu zmaten. Udělal jsem si i obrázek, abych zjistil výsledné řešení a stejně mi to nevychází.
Offline
#4 16. 04. 2020 20:18
Re: Logaritmická nerovnice
↑ nononsense:
Tak já ti to přeložím do češtiny
Pokud řešíš logaritmickou nerovnici (i rovnici), nesmíš zapomenout na podmínky, kdy je logaritmus definovaný (argument logaritmu musí být kladný)
Takže ve tvém příkladě řešíš vlastně soustavu dvou nerovnic
stačí?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 16. 04. 2020 20:57
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
Díky za překlad :D
ano, vím, že nesmím zapomenout na podmínky, ale ty už mám vyřešené (aspoň doufám, že dobře). Je to v mém původním příspěvku, poslední řádek.
Offline
#6 16. 04. 2020 21:18
#7 16. 04. 2020 21:31
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
Tak jak mají teda vypadat podmínky pro  ?
?
Offline
#8 16. 04. 2020 21:35 — Editoval Ferdish (16. 04. 2020 21:36) Příspěvek uživatele Ferdish byl skryt uživatelem Ferdish. Důvod: Nebudem sa kolegom miešať do roboty.
#9 16. 04. 2020 21:43 — Editoval marnes (16. 04. 2020 21:44)
- marnes

- Příspěvky: 11227
Re: Logaritmická nerovnice
↑ nononsense:
Dva nulové body rozdělí osu na tři intervaly. Vem číslo, z jednotlivých intervalů, dosad a zjisti, jestli je nerovnice splněna
Jo. A na začátku vás zdravím.
Offline
#10 16. 04. 2020 21:48
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
Tak jsem zjistil, že nerovnice je splněna v intervalu (2, 3)
Offline
#11 16. 04. 2020 21:49
- marnes

- Příspěvky: 11227
Re: Logaritmická nerovnice
↑ nononsense:
Ok. A dál to máš? Nebo pokračujeme 😁
Jo. A na začátku vás zdravím.
Offline
#12 16. 04. 2020 21:54
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
Asi pokračujeme. Stále mi nedochází, proč je to 
Jinak mám ještě jednu podmínku (x>0), tu jsem zapomněl připsat.
Offline
#13 16. 04. 2020 21:56
#14 16. 04. 2020 21:57
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
↑ marnes:
Tak to platí pro logaritmy, že jsou různé od nuly, nebo ne?
Offline
#15 16. 04. 2020 21:58
#16 16. 04. 2020 21:59 — Editoval marnes (16. 04. 2020 22:00)
- marnes

- Příspěvky: 11227
Re: Logaritmická nerovnice
↑ nononsense:
Tu podmínku jsme ale vyřešili. Místo toho x jsme měli ale náš zlomek
Jo. A na začátku vás zdravím.
Offline
#17 16. 04. 2020 21:59 — Editoval nononsense (16. 04. 2020 22:03)
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
Ta mi vyšla
ale ještě si to radši překontroluji.
edit: tak by to mělo být ok.
Offline
#18 16. 04. 2020 22:07
#19 16. 04. 2020 22:23 — Editoval nononsense (16. 04. 2020 22:24)
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
Tak to nevím, kde mám chybu.
Takhle jsem postupoval: 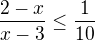

a takhle jsem došel k výsledku.
Offline
#20 16. 04. 2020 22:24
- marnes

- Příspěvky: 11227
Re: Logaritmická nerovnice
↑ nononsense:
Ano. Tak opět nulové body, intervaly, výběr číslo z intervalu a zjisti, ve kterých je splněna nerovnost
Jo. A na začátku vás zdravím.
Offline
#21 16. 04. 2020 22:30
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
↑ marnes:
Konečně! Hrozně moc děkuji a cením si pomoci:) už mi to vyšlo!:D
Offline
#22 16. 04. 2020 22:31
- marnes

- Příspěvky: 11227
Re: Logaritmická nerovnice
↑ nononsense:
Mohu jen vědět jak jsi došel k závěru?
Jo. A na začátku vás zdravím.
Offline
#23 16. 04. 2020 22:38
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Logaritmická nerovnice
↑ marnes:
Udělal jsem si nulové body a intervaly. Pak dělám takovou tabulku, kde píšu + a - pro daný interval. Pak si "sečtu" ty plusy a mínusy a udělám závěr.
Offline
#24 16. 04. 2020 22:48
- marnes

- Příspěvky: 11227
Re: Logaritmická nerovnice
↑ nononsense:
No hlavně že tomu rozumíš sám, já tvému postupů ne.
Osobně bych řešil tu nerovnici a měl bych dva intervaly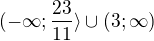
a udělal průnik s podmínkou
Jo. A na začátku vás zdravím.
Offline
