Matematické Fórum

Gauß69 · 19. 04. 2020 19:00

Zdravim,

Nech $f\in C^1(\mathbb{R}^n)$ je konvexna funkcia. Dokaz, ze existuje konstanta $C$ , ktora zavisi len od $n$ , tak ze plati: $\sup_{B_{r/2} (x_0)}\vert f\vert \leq C\int_{B_r (x_0)} \vert f \vert\ dx ,\ \ \ \forall r\in\mathbb{R}, \forall x_0\in\mathbb{R}^n$ .

Moj napad je, vychadzat z toho, ze pre konvexnu funkciu plati $f(y)\geq f(x)+Df(x)\cdot (y-x),\ \ \forall x,y\in\mathbb{R}^n$ . A pomocou toho by som nejako dokazal, ze $\exists C\in\mathbb{R}\ \forall y\in B_{r/2}(x_0):\ f(y)\leq C\int_{B_r (x_0)} \vert f \vert\ dx\ \land \ f(y)\geq -C\int_{B_r (x_0)} \vert f \vert\ dx$ .
Zial ma nenapada ako presne to previest. Ma niekto prosim nejaky napad ako na to?

jardofpr

Ahoj ↑ Gauß69:

len poznamka. Pri praci s konvexnymi funkciami sa casto vyuziva tzv. Hermite-Hadamardova nerovnost
ktora ohranicuje integral konvexnej funkcie z jednej strany hodnotou vnutorneho bodu a z druhej strany
hodnotami bodov na hranici konvexnej oblasti.

Vo vyssich dimenziach predstavuje hodnoty bodov na hranici krivkovy integral, v tvojom pripade
zrejme cez povrch "gule" v $\mathbb{R}^n$ co by znamenalo aj vstup konstanty zavislej na dimenzii do nerovnosti.

S tvojim cvicenim vidim ale trochu problem v tom ze podstatna cast funkcie 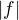$|f|$ sa moze stat
konkavnou ak ma aj zaporne hodnoty a vtedy sa nerovnosti obracaju,
v drvivej vacsine vysledkov sa predpoklada striktne pozitivna konvexna funkcia,
takze mne osobne to zadanie pride trochu zvlastne ked konvexita samotna vlastne nie je plne pouzitelna.

Gauß69 · 20. 04. 2020 12:31

Vdaka za poznamku ↑ jardofpr:

Konvexitu funkcie som vyuzil pri nerovnosti $f(y)\geq f(x)+Df(x)\cdot (y-x)$ .

Trocha som pokrocil od vcera a zadefinoval som si funkciu $\eta (x) =1, \ x\in B_{r/2}(x_0),\ \eta (x) =2-\frac{2\vert x_0-x\vert}{r},\ x\in B_r(x_0)\setminus B_{r/2}(x_0),\ \eta (x) =0,\ x\in\mathbb{R}^n\setminus B_r(x_0)$ . Tato funkcia je ocividne spojita a diferencovatelna, okrem toho zmizne na $\partial B_r(x_0)$ , to budeme potrebovat pri parcialnej integracii.

Teraz vynasobim obidve strany hore spomenutej nerovnice s $\eta(x)$ a obidve strany zintegrujem cez $B_r(x_0)$ . Vdaka parcialnej integracii a par nerovnostiam sa mi podarilo dokazat, ze $f(y)\geq -C\int_{B_r(x_0)}\vert f \vert dx$ , pricom moja konstanta vyzera trocha drasticky, a to $C=\frac{2^n(n+4)\Gamma(\frac{n}{2}+1)}{r^n\pi^\frac{n}{2}}$ .

Kazdopadne mi nic lepsie nenapadlo, a stale mi zostava dokazat, ze $f(y)\leq C\int_{B_r(x_0)}\vert f \vert dx$ .

Matematické Fórum

#1 19. 04. 2020 19:00

Nerovnica integralu konvexnej funkcie

#2 20. 04. 2020 11:24 — Editoval jardofpr (20. 04. 2020 11:31)

Re: Nerovnica integralu konvexnej funkcie

#3 20. 04. 2020 12:31

Re: Nerovnica integralu konvexnej funkcie

Zápatí