Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 04. 2020 03:27
Re: Vrcholové zafarbenia grafov
Ahoj, ja bych zacal tak, ze bych si rozmyslel, jak vypada graf, ktery pro dane X(G) a n ma maximalni pocet hran.
Dosel bych k zaveru, ze takovy graf ma priblizne stejny pocet vrcholu (p nebo p+1) ruznych barev, tj
a vsechny ruzne barevne vrcholy jsou spojeny. Pocet hran, ktere chybi do uplneho grafu je pak rovny poctu hran,
ktere je nutno pridat mezi stejnebarevne vrcholy a plati tedy odhad
Dosadime-li za 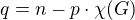 , ziskame
, ziskame
coz lze prepsat na 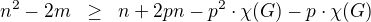
a staci tedy ukazat, ze plati
coz lze zapsat jako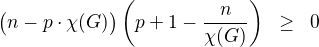
Prvni zavorka je rovna  a je urcite nezaporna, druha zavorka je rovna
a je urcite nezaporna, druha zavorka je rovna  .
.
Offline