Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 04. 2020 10:11
Gravitační pole
Zdravím,
potřebovala bych poradit s následujícím příkladem:
Vzdálenost mezi hmotnými středy Země a Měsíce je d, viz Obrázek 1. Hmotnost Měsíce je 1/81 hmotnosti Země. Určete:
a) v jaké vzdálenosti x1 od středu Země je intenzita společného gravitačního pole (Eg,z a Eg,m ) rovna nule,
b) v jaké vzdálenosti x2 od středu Země je potenciál gravitačního pole Země (φz) dvakrát větší než tatáž veličina Měsíce (φm).
a) 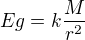
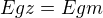
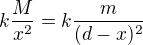

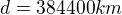
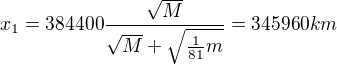
b)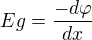
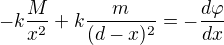

Tada nevím jak pokračovat dál
Offline