Matematické Fórum

Ell111 · 03. 05. 2020 22:42

Dobrý deň, vedel by mi prosím vás niekto poradiť ako by sa dala vypočítať táto funkcia podľa Lagrangeovej vety? ďakujem pekne za odpoveď. f(x)=lnx , x patrí [e,2e]

vlado_bb · 03. 05. 2020 22:44

↑ Ell111:Teda ako najst jej strednu hodnotu na intervale $[e,2e]$ ? Napis, co hovori Lagrangeova veta a z toho to uz snad uvidime.

Ell111 · 04. 05. 2020 09:46

$\int_{a}^{b} f(x) dx /b-a Lagrangeova veta ∫baf(x)dx/b−a$

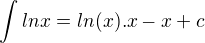Najprv som ten určitý integral vypočítalaako neurčitý integral $\int_{}^{} lnx=ln(x).x-x+c$ čo mi vyšlo takto, potom podla vzorca určiteho integralu mi vyšlo toto 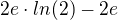$2e\cdot ln(2)-2e$ a teraz neviem či to tak má byt ale vložila by som to do toho Lagrangeoveho vzorca