Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 05. 2020 15:43
Orientované grafy
Dobrý deň,
vedel by mi niekto pomôcť s touto úlohou?
Nech G je neorientovaný graf. Dokážte, že jeho hrany možno zorientovať tak, aby vo výslednom digrafe D platilo
|deg+(v) − deg−(v)| ≤ 1 pre každý vrchol v ∈ V (D).
Ďakujem
Offline
- (téma jako vyřešené označil(a) jajko)
#2 08. 05. 2020 02:37 — Editoval nejsem_tonda (08. 05. 2020 02:41)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Orientované grafy
↑ jajko:
Ahoj,
premyslim o tom tak, ze bych chtel vyuzit indukci podle poctu vrcholu. Takze bych chtel odebrat jeden vrchol (i s jeho hranami), ze zbytku udelat vhodny orientovany graf a ten vrchol zpatky pridat a nejak vhodne zorientovat jeho hrany. Uplne primocare to asi nepujde, takze to zkusim takhle:
1) Kdykoliv v grafu najdu kruznici, muzu hrany te kruznice zorientovat vsechny stejnym smerem a v ramci te kruznice plati pro kazdy vrchol v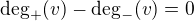 (obe to jsou jednicky)
(obe to jsou jednicky)
Jinymi slovy kdyz tu kruznici z grafu odeberu a podari se mi zorientovat zbytek, muzu pak tu kruznici zpatky pridat (vsechny jeji hrany zorientuju jednim smerem) a dostanu zase dobre zorientovany graf.
2) Vyberu si tedy vrchol V, ktery chci z grafu odebrat (a na zbytek pouzit indukci). Predtim nez vrchol V odeberu, se podivam, jestli pres nej prochazi nejaka kruznice. Pokud ano, vyberou kteroukoliv kruznici obsahujici V a vsechny jeji hrany z grafu odeberu. Toto opakuju tak dlouho, dokud pres V neprochazi zadna kruznice.
3) Ted mam graf, ve kterem zadna kruznice neprochazi pres V. Muze vypadat nejak takto: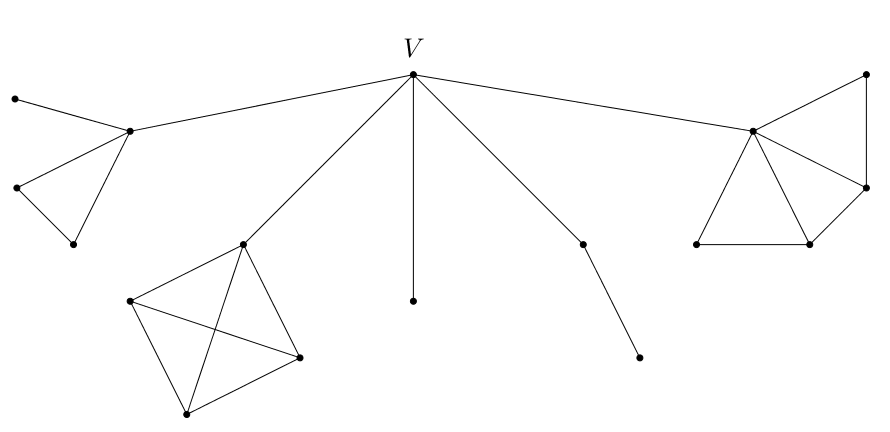
4) Mnozinu sousedu vrcholu V oznacim S. Urcite vim, ze mezi vrcholy z S nevede zadna hrana, protoze jinak by existovala kruznice (dokonce trojuhelnikova) pres V. Ted prijde hlavni trik:
Vrcholy z S si rozdelim libovolne do dvojic a kazdou dvojici spojim cervenou hranou.
Pokud mel V lichy stupen, jeden vrchol z S zustane nesparovany. Zaroven smazu vsechny hrany vedouci z V. Nas graf by ted vypadal napriklad takto (nesparovany vrchol je ten byvaly soused V, ktery je nejvice vlevo).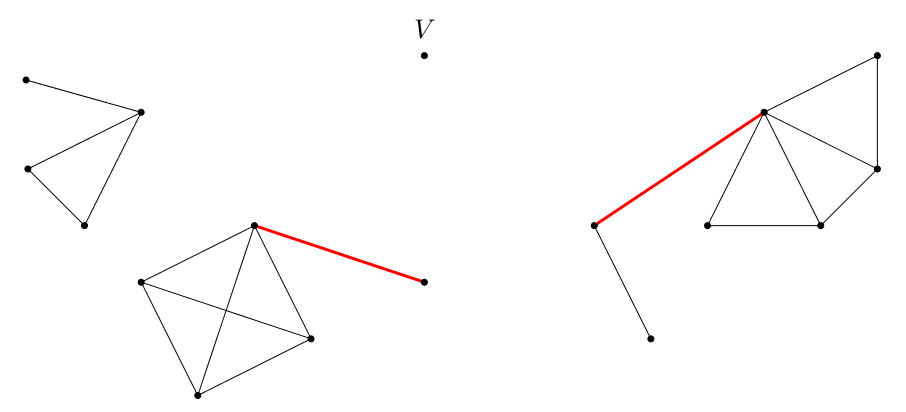
5) Ted konecne muzu na zbyvajici graf pouzit indukci, protoze mam o vrchol mene. Indukce mi jej nejak vhodne zorientuje. Napriklad to muze dopadnout takto:
6) Vratim se k puvodnimu grafu. To znamena, ze odeberu kazdou cervenou hranu a nahradim ji dvojici cervenych hran vedouci pres V. Zorientuju je tak, jak byla zorientovana cervena hrana. Tim zajistim, ze kazdemu vrcholu z mnoziny S, ktery byl sparovany, jsem nezmenil  , ani
, ani 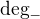 . Jinymi slovy v grafu bez fialove hrany spojujici V a nesparovany vrchol (muze a nemusi existovat) je z indukcniho predpokladu zajistena nerovnost
. Jinymi slovy v grafu bez fialove hrany spojujici V a nesparovany vrchol (muze a nemusi existovat) je z indukcniho predpokladu zajistena nerovnost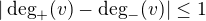

7) Zbyva okomentovat fialovou hranu. Pokud ji neuvazuju, plati pro V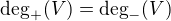
Vrcholu V je tedy jedno, v jakem smerem fialovou hranu zorientuju. Nesparovanemu vrcholu to jedno byt nemusi. Napriklad v nasem grafu jsme fialovou hranu museli zorientovat smerem do V.
8) Nakonec do grafu pridam vsechny ty kruznice, ktere jsem odebral v kroku 2. Ty nemuzou nic pokazit.
Je to trochu dlouhe. Treba nekdo vymysli jednodussi postup.
Offline
#3 08. 05. 2020 11:59
Re: Orientované grafy
↑ jajko:
Ahoj. Ja bych proste odebiral z grafu kruznice, dokud to jde. Ziskam tak graf bez kruznic - les. Tvrzeni tedy staci dokazat pro strom. Vyberu si libovolny vrchol stromu a (napr.) po smeru hodinovych rucicek zorientuju nastridacku hrany. Pak pokracuju se sousednimi vrcholy, pricemz se zorientovanim zacinam od jiz zorientovane hrany. Opet stridam orientaci hran. Tak postupuju az k listum.
Offline
#4 19. 05. 2020 14:38
Re: Orientované grafy
↑ jajko:Myslím, že nejelegantnější řešení je využít orientaci eulerovského tahu, který najdeme v každé komponentě sudého grafu . Pokud graf není sudý, přidáme pomocný vrchol a hranou jej spojíme s každým vrcholem lichého stupně. Odstraněním pomocného vrcholu v orientaci sudého grafu máme hledanou orientaci původního grafu.
Offline