Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Globální extrémy funkce více proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 05. 2020 15:00
Globální extrémy funkce více proměnných
Dobrý den,
počítám extrémy funkce více proměnných. Máme vypočítat lokální i globální extrémy zadaných funkcí. Zadaná je pouze ale funkce dvou proměnných a nikde žádná oblast (podmínky). Podle videí, ze kterých se učím, mají vždy nějaké omezení, když počítají ty globální extrémy. Znamená to tedy, že mé zadání mám prostě brát tak, že vezmu globální extrém = lokální extrém?
Moc děkuju. :)
Offline
- (téma jako vyřešené označil(a) Tom01)
#2 14. 05. 2020 16:32 — Editoval surovec (14. 05. 2020 16:34)
Re: Globální extrémy funkce více proměnných
↑ Tom01:
Tím lokálním extrémem myslí nějaký "kopeček" nebo "dolíček". Vrchol toho kopečku je maximem na nějakém okolí, ale to neznamená, že někde není ještě vyšší kopeček nebo dokonce nekonečně rostoucí kopec, nebo někde vysoko letící "balón" (izolovaný bod) apod. Každopádně v tom lokálním kopečku jsou (pokud existují) parciální derivace nulové. Když je kopeček nějak špičatý, mohou tam být některé parciální derivace nulové a některé neexistují...
Offline
#3 14. 05. 2020 19:04
Re: Globální extrémy funkce více proměnných
↑ surovec:
Ano, ale pokud je tedy funkce spojitá, mohu vycházet z toho, že můj lokální extrém stanovím na celém definičním oboru jako globální extrém? Protože žádné omezení v zadání není ...
Ještě jednou díky. :)
Offline
#4 14. 05. 2020 19:24
Re: Globální extrémy funkce více proměnných
↑ Tom01:Ano, globalny extrem je najvacsia hodnota na mnozine, na ktorej funkciu skumame, v tomto pripade teda na celom priestore. Globalne maximum teda moze byt maximum z lokalnych maxim, ale pozor - toto maximum nemusi existovat, a to ani pre ohranicenu funkciu (napriklad funkcia typu 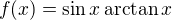 ) a takisto pozor na to, ze spojitost funkcie este nezarucuje jej diferencovatelnost, a teda globalny extrem moze byt aj v bode, kde derivacia neexistuje (funkcia typu
) a takisto pozor na to, ze spojitost funkcie este nezarucuje jej diferencovatelnost, a teda globalny extrem moze byt aj v bode, kde derivacia neexistuje (funkcia typu 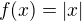 ).
).
Offline
#6 14. 05. 2020 21:06
Re: Globální extrémy funkce více proměnných
↑ vlado_bb:↑ surovec:
Už to chápu. Vyberu z těch lokálních extrémů ty s nejmenší/největší funkční hodnotou (za předpokladu, že existují), a to bude to globální minimum/maximum.
Jen mě ještě napadlo ... když vidím ten obrázek ... globální maximum neexistuje, ale jak zjistím, že toto lokální maximum není globálním maximem (když nebudu vědět, jak vypadá graf funkce ... mám počítat limity do +/- nekonečna?
Díky oboum. :)
Offline
#8 14. 05. 2020 21:43
Re: Globální extrémy funkce více proměnných
↑ vlado_bb:
Ok, takže potom postupuji tak, že existuje-li nějaká limita (v nevlastních bodech), která jde do + nekonečna / - nekonečna, vím, že globální maximum / globální minimum nebude existovat?
Díky. :)
Offline
#10 14. 05. 2020 22:05
Re: Globální extrémy funkce více proměnných
↑ surovec:
Ok, díky všem moc za vysvětlení a pomoc. :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Globální extrémy funkce více proměnných (TOTO TÉMA JE VYŘEŠENÉ)

