Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » nesudelitelne cisla (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 10. 2009 19:18
- matikajesuper
- Zelenáč
- Příspěvky: 2
- Reputace: 0
nesudelitelne cisla
Tak takú úlohu mám vypočítať za domácu úlohu som prvák na mat. gympli. Neviem si s nou rady
Offline
#2 06. 10. 2009 10:29 — Editoval Pavel (06. 10. 2009 10:32)
Re: nesudelitelne cisla
↑ matikajesuper:
Nechť  a nechť
a nechť  a
a  jsou nesoudělná, tedy
jsou nesoudělná, tedy  . Pak
. Pak  . Aby tento zlomek byl celé číslo, musí být čitatel dělitelný 9. To bude platit jen tehdy, když
. Aby tento zlomek byl celé číslo, musí být čitatel dělitelný 9. To bude platit jen tehdy, když  . Pak
. Pak . Protože je jmenovatel dělitelný číslem
. Protože je jmenovatel dělitelný číslem  , musí být i čitatel dělitelný číslem
, musí být i čitatel dělitelný číslem  . To bude platit tehdy, když
. To bude platit tehdy, když  nebo
nebo  . Kdyby pro
. Kdyby pro  platilo, že
platilo, že  , bylo by to ve sporu s nesoudělností čísel
, bylo by to ve sporu s nesoudělností čísel  a
a  .
.
Tudíž pro  platí
platí  , a tedy nemůže platit
, a tedy nemůže platit  . Pak není jiná možnost než
. Pak není jiná možnost než 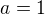 nebo
nebo  . Tzn.
. Tzn.  .
.
1. Nechť 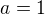 . Pak
. Pak 
Protože je jmenovatel dělitelný číslem  , musí platit, že
, musí platit, že  . To platí jen tehdy, když
. To platí jen tehdy, když  . To dává hodnotu
. To dává hodnotu 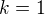 . Jedno z řešení je
. Jedno z řešení je
2. Nechť 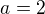 . Pak
. Pak 
Protože je jmenovatel dělitelný číslem  , musí platit, že
, musí platit, že  . To platí jen tehdy, když
. To platí jen tehdy, když  .. To spolu s
.. To spolu s  dává hodnotu
dává hodnotu 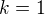 .
. 
3. Nechť 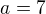 . Pak
. Pak 
Protože je jmenovatel dělitelný číslem  , musí platit, že
, musí platit, že  . To platí jen tehdy, když
. To platí jen tehdy, když  . To spolu s
. To spolu s  dává hodnotu
dává hodnotu 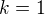 .
. 
4. Nechť  . Pak
. Pak 
Protože je jmenovatel dělitelný číslem  , musí platit, že
, musí platit, že  . To platí jen tehdy, když
. To platí jen tehdy, když  . To spolu s
. To spolu s  dává hodnotu
dává hodnotu 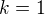 .
. 
Existují tedy 4 řešení, pokud  a
a  jsou nesoudělná. Pokud by byla soudělná, existovalo by nekonečně mnoho řešení. Řeší-li totiž úlohu čísla
jsou nesoudělná. Pokud by byla soudělná, existovalo by nekonečně mnoho řešení. Řeší-li totiž úlohu čísla  a
a  , pak ji řeší také čísla
, pak ji řeší také čísla  a
a  ,
,  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 06. 10. 2009 11:01 — Editoval musixx (06. 10. 2009 11:16)
Re: nesudelitelne cisla
Možná trošku rychleji:  je celé, jen když je čitatel dělitelný:
je celé, jen když je čitatel dělitelný:
A)  , což dává
, což dává  ,
,
B)  , což spolu s
, což spolu s  dává
dává  ,
,
C)  , což spolu s
, což spolu s  dává
dává  .
.
Kdyby 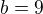 , pak je jmenovatel dělitelný 81,
, pak je jmenovatel dělitelný 81,  taktéž, tedy
taktéž, tedy  , tedy
, tedy  spor s
spor s  . Je tedy
. Je tedy 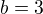 , protože hledáme jen kladná řešení.
, protože hledáme jen kladná řešení.
Stačí prověřit, pro která kladná  je
je  celé (ukáže se, že pro všechna
celé (ukáže se, že pro všechna  ).
).
EDIT: (s tušením o kongruencích čistě jen pro snažší zápis) Dokonce je jasné, že  , tedy by stačilo prověřovat, kdy
, tedy by stačilo prověřovat, kdy  , tedy
, tedy  , ovšem z
, ovšem z  máme
máme  , tedy vlastně není co prověřovat, protože
, tedy vlastně není co prověřovat, protože  je zaručeno pro
je zaručeno pro  .
.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » nesudelitelne cisla (TOTO TÉMA JE VYŘEŠENÉ)
