Matematické Fórum

Andrew123

Ahoj,
mel bych dotaz ohledne vypoctu vyberoveho rozptylu. Pro pripomenuti jedna z moznosti, jak ho spocitat, je nasledujici: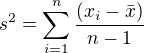

$s^2=\sum_{i=1}^{n}\frac{(x_i-\bar{x})}{n-1}$ .

Chtel bych se zeptat na vysvetleni deleni vysledneho souctu $n-1$ a ne $n$ . Na internetu jsem sice nasel pomerne dost vysvetleni, proc se to tak deli, aby odhad byl nestranny, ale v jedne publikaci (Probability and statistics for engineeers and scientists, 8ed, Walpole, ...), kterou jsem zacal cist, to vysvetluji zpusobem, kterym nerozumim, byt ocekavam, ze by to slozite byt nemelo. Jedna se totiz uplne o uvod do statistiky v prvni kapitole knihy.. Pokusim se tu cast volne preformulovat z anglictiny:

----------------------------
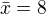Hodnota $n-1$ se nazyva stupen volnosti rozptylu. Stupen volnosti vystihuje pocet nezavislych casti pro vypocet. Napr., predpokladejme, ze chceme spocitat vyberovy rozptyl a smerodatnou odchylku dat (5, 17, 6, 4). Jejich prumer je $\bar{x}=8$ . Vypocet rozptylu zahrnuje:
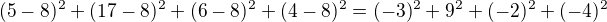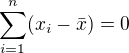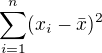$(5-8)^2 + (17-8)^2 + (6-8)^2 + (4-8)^2 = (-3)^2 + 9^2 + (-2) ^2 + (-4)^2$ . Vyrazy uvnitr zavorek davaji v souctu nulu. Obecne je $\sum_{i=1}^{n}(x_i-\bar{x})=0$ . $n$ částí v $\sum_{i=1}^{n}(x_i-\bar{x})^2$ neni nezavisla. Potom vypocet vyberoveho rozptylu nezahrnuje $n$ nezavislych ctvercovych odchylek od stredni hodnoty. Ve skutecnosti, posledni hodnota $x-\bar{x}$
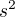je urcena $n-1$ z nich. Rikame, ze techto $n-1$ casti vytvareji $s^2$ . Tedy, je to $n-1$ stupnu volnosti spise nez $n$ stupnu volnosti pro vypocet vyberoveho rozptylu.
---------------------------

Z tohoto textu vyse vubec nerozumim, proc je $n-1$ casti nezavislych a $n$ casti uz neni nezavisly a dale, jak s tim souvisi deleni souctu vyrazem $n-1$ a ne vyrazem $n$ . Proc je $n-1$ casti nezavislych a $n$ casti uz ne? Jak to vysvetluje to, proc je rozptyl deleny $n-1$ ? Nerad bych to preskocil a rad bych to pochopil.

Poradite prosim nekdo? Dekuji.

kastanek · 16. 06. 2020 13:24

↑ Andrew123:
Tak tohle mě také vždy zajímalo, proč tam je to n-1. Rád si počkám na polopatickou odpověď...

Brano · 16. 06. 2020 14:03

To vysvetlenie v skutocnosti nie je vysvetlenie ale skor mnemotechnicka pomocka.

Ked sa to odvadza poriadne (co si uz bohuzial do detailu nepamatam), tak sa v dokaze objavi, ze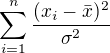
$\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{\sigma^2}$ ma rozdelenie 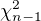$\chi^2_{n-1}$ pricom to $n-1$ v postupe vyjde ako pocet nezavyslych stlpcov v nejakej matici.

Taketo chovanie je typicke vzdy ked sa objavuje $\chi^2$ - preto sa aj ten parameter vola "stupne volnosti"
(ak niekto viete ako sa ta veta co sa za tym skryva vola tak prosim dajte odkaz).

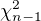No a potom ak chces nevychyleny odhad $\sigma^2$ tak sa v menovateli objavi $n-1$ lebo to je stredna hodnota $\chi^2_{n-1}$ . A este potom musis dokazat, ze sa jedna o najlepsi nevychyleny odhad :-P.

Odhad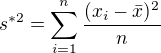
$s^{*2}=\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{n}$
dostanes inak. Kontretne ako maximalne vierohodny co je iny postup.

nejsem_tonda

↑ Andrew123:
Ahoj,
nedavno jsem o tom psal k jednomu jinemu zdejsimu dotazu, tak odpoved uz jenom zkopiruju.

Pro porozumeni, proc to tak je, doporucuju precist si o Besselove korekci, predevsim odstavec Source of bias. Na zaver si jeste rozklikni Proof of correctness – Alternative 3, kde je vysvetlujici odstavec Intuition.

Mas-li k tomu nejake dotazy, klidne pis, ale cele to tady opisovat by mi prislo zbytecne - zvlast kdyz je to na wikipedii vysvetlene celkem pekne.

Z tohoto textu vyse vubec nerozumim, proc je $n-1$ casti nezavislych a $n$ casti uz neni nezavisly

To se ti nedivim - to, cos tady zkopiroval, nemuze byt seriozni matematicky text. Zacni cist neco poradneho ;-)
Mluvit v tomto kontextu o n-1 nezavislych castech podle me nedava smysl.

Andrew123 · 17. 06. 2020 19:39

↑ nejsem_tonda:

Ahoj, dekuji za odkaz.. Juknu na to a kdyztak napisu.. Tuto publikaci jsem zacal cist, protoze na Amazonu ma celkem dobre reference a pro bakalarsky predmet aplikovana statistika na VSCHT je uvedena jako literatura doporucena (krome skript).. Navic se mi podarilo sehnat solution/instructor manual k teto publikaci.., tak tomu dam jeste sanci..:-)

Matematické Fórum

#1 16. 06. 2020 12:30 — Editoval Andrew123 (16. 06. 2020 12:33)

Vyberovy rozptyl - deleni souctu n-1

#2 16. 06. 2020 13:24

Re: Vyberovy rozptyl - deleni souctu n-1

#3 16. 06. 2020 14:03

Re: Vyberovy rozptyl - deleni souctu n-1

#4 17. 06. 2020 00:23 — Editoval nejsem_tonda (17. 06. 2020 00:54)

Re: Vyberovy rozptyl - deleni souctu n-1

#5 17. 06. 2020 19:39

Re: Vyberovy rozptyl - deleni souctu n-1

Zápatí