Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 06. 2020 13:37
Determinant
Nech A,B su komplexne matice typu nxn a AB-BA=A.
Urcite det A.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 16. 06. 2020 14:17 — Editoval laszky (02. 07. 2022 02:47)
#4 18. 06. 2020 19:49
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Determinant
Zkusím toto poloviční řešení:
"Máte úhel beta." "No to nemám."
Offline
#5 19. 06. 2020 00:35 — Editoval vanok (19. 06. 2020 10:19)
Re: Determinant
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 19. 06. 2020 16:10
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Determinant
↑ vanok:
Ahoj, děkuji. Já jsem se snažil použít co nejméně netriviálních tvrzení, využij jsem vlastně zatím jen tvrzení o distributivitě násobení matic a o součinu determinantů.
"Máte úhel beta." "No to nemám."
Offline
#7 19. 06. 2020 16:59
Re: Determinant
Cau ↑ check_drummer:,
No a tak ak ti ide o dokoncenie «tvojho » dokazu, ze  , staci pouzit vlasnosti Tr.
, staci pouzit vlasnosti Tr.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

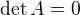 .
.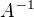 matice
matice  existuje je ekvivalentne z tym, ze jej det je nenulovy.
existuje je ekvivalentne z tym, ze jej det je nenulovy.