Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#27 10. 07. 2020 19:42 — Editoval Dacu (10. 07. 2020 19:46)
Re: Systém diferenciálních rovnic
vlado_bb napsal(a):
↑↑ Dacu:Of course he is wrong,
and
are not roots of
.
Hello,
I made the same mistake and you saw that I corrected it ....Bati had to write 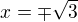 ....
....
It is wrong what Bati says, namely:
"Let 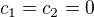 Then
Then  for all
for all 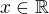 " referring to the functions
" referring to the functions  and
and  ?
?
vlado_bb napsal(a):
↑↑ Dacu:Such functions do not exist (see the solution by ↑↑ jarrro:).
I repeat:
I think that one solution could be  and
and  .
.
Please kindly prove to me that the above solution is not correct!Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#28 10. 07. 2020 20:30 — Editoval vlado_bb (10. 07. 2020 20:35)
Re: Systém diferenciálních rovnic
↑ Dacu:The proof by jarrro is very clear. Which part you do not understand?
Your functions 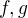 can only exist on the set
can only exist on the set  . However, they have not derivatives of this set, so they cannot be the solution of your system. So, there is no solution.
. However, they have not derivatives of this set, so they cannot be the solution of your system. So, there is no solution.
Offline
#29 28. 07. 2020 16:50
Re: Systém diferenciálních rovnic
↑ Dacu:
I made an oversight, sorry for that. However, my conclusion remains the same. If 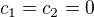 , then your system becomes
, then your system becomes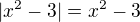

The first equality is true iff ![kopírovat do textarea $x\in (-\infty,-\sqrt3]\cup[\sqrt3,\infty)$](/mathtex/4d/4da9a134eb33ed54d573458716818c56.gif) , while second is true iff
, while second is true iff ![kopírovat do textarea $x\in[-\sqrt3,\sqrt3]$](/mathtex/90/902406c2d7c9f697fe0c1428b7daf410.gif) . So your particular ``solution'' works only at points
. So your particular ``solution'' works only at points 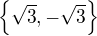 (which could be achieved by a much simpler function if thats what you want)
(which could be achieved by a much simpler function if thats what you want)
Offline
#31 28. 07. 2020 18:40
Re: Systém diferenciálních rovnic
↑ vlado_bb:
Functions f,g from #21 are defined (and smooth) everywhere
Offline
#33 28. 07. 2020 23:15
Re: Systém diferenciálních rovnic
↑ vlado_bb:
I would say no to that... those functions are defined in R and whether they solve something or not is irrelevant in that regard. But this debate is rather pointless, I just wanted to provide a direct argument which I believe Dacu was asking for. jarrro's answer is completely fine as well, of course
Offline
#34 29. 07. 2020 07:24 — Editoval Dacu (29. 07. 2020 07:29)
Re: Systém diferenciálních rovnic
Hello all,
From the "WolframAlpha" read:
Odkaz
Is it correct what "WolframAlpha" displays? I say yes!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#35 29. 07. 2020 09:29
Re: Systém diferenciálních rovnic
Hi ↑ Dacu:
I say resolute NO. Lets find the minimal (un)working example: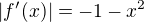
I hope that you agree that there exist no functions f solving this equation (as the left side is always >=0, but right side is always <0
But wolfram says:

And it is also obvious what it does wrong: It writes  , which is fine, but then it squares both sides of equation to convert it to a ''standard'' form, which however results in a very different ODE then the original one (simply because
, which is fine, but then it squares both sides of equation to convert it to a ''standard'' form, which however results in a very different ODE then the original one (simply because  is not equivalent to
is not equivalent to  etc.)
etc.)
You should never trust blindly these computational engines. They are written (at least initially) by people and it is very difficult, if not impossible, to write it in a way that it processess any mathematically valid input. These tools, however, can be very useful for checking your intuition or your computations. That said, they can not think for you (yet).
Still, you may try to report this bug to WA. The desktop version of wolfram produces the same result:
DSolve[Abs[f'[x]] == -1 - x^2, f[x], x]
gives the same output as WA, but with a small warning:
Solve::ifun: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information.
Curiously enough, wolfram gives the right answer to  (again, no solution).
(again, no solution).
Offline
#36 30. 07. 2020 06:30
Re: Systém diferenciálních rovnic
Bati napsal(a):
Hi ↑ Dacu:
I say resolute NO. Lets find the minimal (un)working example:
I hope that you agree that there exist no functions f solving this equation (as the left side is always >=0, but right side is always <0
But wolfram says:
And it is also obvious what it does wrong: It writes, which is fine, but then it squares both sides of equation to convert it to a ''standard'' form, which however results in a very different ODE then the original one (simply because
is not equivalent to
etc.)
You should never trust blindly these computational engines. They are written (at least initially) by people and it is very difficult, if not impossible, to write it in a way that it processess any mathematically valid input. These tools, however, can be very useful for checking your intuition or your computations. That said, they can not think for you (yet).
Still, you may try to report this bug to WA. The desktop version of wolfram produces the same result:
DSolve[Abs[f'[x]] == -1 - x^2, f[x], x]
gives the same output as WA, but with a small warning:
Solve::ifun: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information.
Curiously enough, wolfram gives the right answer to(again, no solution).
Hello,
I think that for 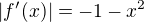 the answer https://www.wolframalpha.com/input/?i=% … 3D-1-x%5E2 is correct , because it considers that
the answer https://www.wolframalpha.com/input/?i=% … 3D-1-x%5E2 is correct , because it considers that  ,
, 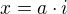 ,
, 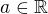 and
and 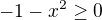 ...
...
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#37 30. 07. 2020 08:03 — Editoval Bati (30. 07. 2020 08:05)
Re: Systém diferenciálních rovnic
↑ Dacu:
Even if this was true, this function  cannot be a solution on the whole line
cannot be a solution on the whole line 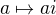 (it fails in
(it fails in 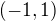 ). At any case, you really should specify this
). At any case, you really should specify this 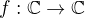 first and then you should also explain what do you mean by a solution (for someone, it may be not enough that the solution works only pathwise). I think your system becomes a usual real ODE system after applying a simple substitution and so there is no reason to assume you haven't applied it already.
first and then you should also explain what do you mean by a solution (for someone, it may be not enough that the solution works only pathwise). I think your system becomes a usual real ODE system after applying a simple substitution and so there is no reason to assume you haven't applied it already.
Offline
