Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 08. 2020 13:31
Velká Fermatova věta
Ahoj.
Prosím mohl by se někdo podívat, jestli v následujícím nemám nějakou chybu? Děkuji :) Všechno by to měly být jen čistě středoškolské operace, žádná vysoká matematika.
Nechť  ,
,  a
a  jsou po dvou nesoudělná čísla a
jsou po dvou nesoudělná čísla a 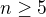 je prvočíslo. Dále nechť
je prvočíslo. Dále nechť 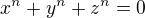 .
.
Úpravami dostaneme:
(1) 
(2) 
Nyní uveďme pomocné tvrzení. Pro libovolná nesoudělná  ,
,  a prvočíselné
a prvočíselné  platí, že každý dělitel čísla
platí, že každý dělitel čísla  je buď
je buď  nebo je tvaru
nebo je tvaru 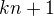 pro nějaké celočíselné
pro nějaké celočíselné 
Důkaz není tak obtížný a na požádání ho uvedu. Tady by ale zbytečně zabíral místo a činil celý text méně přehledným.
Nyní definujme pro celočíselné  hodnotu
hodnotu  jako největší celé číslo takové, že
jako největší celé číslo takové, že  nedělí
nedělí  a současně žádný z dělitelů čísla
a současně žádný z dělitelů čísla  není tvaru
není tvaru  pro celočíselné
pro celočíselné  .
.
Všimněme si že pro naši definici pak platí, že ať už jsou  ,
,  libovolná nesoudělá čísla, tak
libovolná nesoudělá čísla, tak 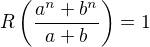 . Dále si všimněme zjevného faktu
. Dále si všimněme zjevného faktu 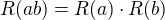
S využitím předchozího máme a vztahů (1) a (2):
- 
- 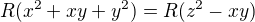
Díky symetrii v  ,
,  a
a  potom dostaneme zajímavý vztah (a zároveň definici pro
potom dostaneme zajímavý vztah (a zároveň definici pro  :
:
(3) 
Zjevně pro každé  platí, že
platí, že  dělí
dělí  , což dostaneme přímo z definice. Díky tomu máme, že
, což dostaneme přímo z definice. Díky tomu máme, že  dělí
dělí  a současně
a současně  dělí
dělí  , dělí i tedy jejich rozdíl, což je
, dělí i tedy jejich rozdíl, což je 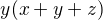 . Vzhledem k nesoudělnosti
. Vzhledem k nesoudělnosti  ,
,  a
a  a faktu, že
a faktu, že  dělí
dělí 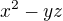 dostaneme:
dostaneme:
(4)  dělí
dělí 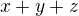
Protože  dělí
dělí 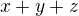 a současně
a současně  dělí
dělí  , musí
, musí  dělit též
dělit též 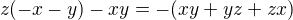 . Proto s využitím (4) dostaneme:
. Proto s využitím (4) dostaneme:
(5) Definujme 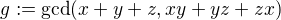 . Pak
. Pak  dělí
dělí  .
.
Hodnota  je největší společný dělitel
je největší společný dělitel 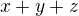 a
a  , proto
, proto  dělí též
dělí též  . Tedy
. Tedy  dělí
dělí  . Odsud plyne, že
. Odsud plyne, že 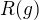 dělí
dělí  . Přitom ale i
. Přitom ale i  dělí
dělí 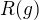 , protože už víme, že
, protože už víme, že  dělí
dělí  díky (5). Proto platí
díky (5). Proto platí
(6) 
V tomto vlákně budu případně pokračovat. Nejprve bych ale poprosil, jestli by se někdo nepodíval, jestli není chyba v nějakém z těchto kroků. Já jsem to dotáhl až do "důkazu" Velké Fermatovy věty, takže někde chyba pravděpodobně je :D Jen jde o to ji najít. Za každé přečtení moc děkuju :)
Offline
#2 15. 08. 2020 16:04 — Editoval check_drummer (15. 08. 2020 16:14)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
liamlim_2 napsal(a):
Nyní uveďme pomocné tvrzení. Pro libovolná nesoudělná
,
a prvočíselné
platí, že každý dělitel čísla
je buď
nebo je tvaru
pro nějaké celočíselné
Ahoj, nevidím nikde použití toho  . Dále pro a=1, b=-1 dostaneme ve jmenovateli 0.
. Dále pro a=1, b=-1 dostaneme ve jmenovateli 0.
"Máte úhel beta." "No to nemám."
Offline
#3 15. 08. 2020 16:17
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta

Pro x=1, y=1 dostanem 0 ve jmenovateli.
"Máte úhel beta." "No to nemám."
Offline
#4 15. 08. 2020 16:19
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
Proč platí tato rovnost?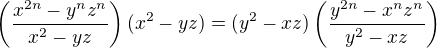
"Máte úhel beta." "No to nemám."
Offline
#5 15. 08. 2020 16:38 Příspěvek uživatele liamlim_2 byl skryt uživatelem liamlim_2.
#6 15. 08. 2020 16:40 — Editoval liamlim_2 (15. 08. 2020 16:40)
Re: Velká Fermatova věta
↑ check_drummer:
Pokud jsou  ,
,  různá nesoudělná čísla a
různá nesoudělná čísla a  je prvočíslo větší nebo rovno 5, pak platí
je prvočíslo větší nebo rovno 5, pak platí  má pouze dělitele tvaru
má pouze dělitele tvaru 
Offline
#7 15. 08. 2020 16:42
#8 15. 08. 2020 16:43
Re: Velká Fermatova věta
↑ check_drummer: a
a  nemůžou být obě 1, protože pak z
nemůžou být obě 1, protože pak z  dostaneme
dostaneme  , což není možné
, což není možné
Offline
#10 15. 08. 2020 17:36
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
↑ liamlim_2:
Je hodnota R(a) korektně definována? Tj. existuje vždy R(a), tj. nemohou být čísla splňující definici R(a) "neomezeně velká"?
"Máte úhel beta." "No to nemám."
Offline
#12 15. 08. 2020 18:01
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
↑ liamlim_2:
V textu výše ale není uevdeno, že R(a) je dělitelem čísla a.
"Máte úhel beta." "No to nemám."
Offline
#13 15. 08. 2020 18:12
Re: Velká Fermatova věta
↑ check_drummer:
Ano to mi vypadlo, za to se omlouvám. Samozřejmě  musí být dělitel čísla
musí být dělitel čísla  . Chtěl bych opravit chyby a editovat text výše, možnost editace ale nevidím.
. Chtěl bych opravit chyby a editovat text výše, možnost editace ale nevidím.
Offline
#14 15. 08. 2020 20:46 — Editoval misaH (15. 08. 2020 20:47)
- misaH
- Příspěvky: 13431
Re: Velká Fermatova věta
možnost editace ale nevidím
Pravý dolný roh okna - ty tam nemáš
Reagovat ... Editovat ... .... ?
Offline
#16 15. 08. 2020 23:04
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
↑ liamlim_2:
Napiš do sekce "Přivolej si svého admina" nebo jak se to jmenuje. Každý by měl mít možnost editovat své příspěvky... Nemám rád nástroje, kde můžeš svůj příspěvěk jen smazat, ale nemůžeš ho editovat. Někdy to dává smysl, když na tebe jiní reagují, ale jak říkám, nemám to rád. :-)
"Máte úhel beta." "No to nemám."
Offline
#17 15. 08. 2020 23:46 — Editoval check_drummer (15. 08. 2020 23:48)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
liamlim_2 napsal(a):
Nyní definujme pro celočíselné
hodnotu
jako největší celé číslo takové, že
nedělí
a současně žádný z dělitelů čísla
není tvaru
pro celočíselné
.
Pro k=0 získáme číslo 1 a to je dělitel každého čísla, takže R(a) není správně definováno. A i když vyloučíš případ k=0, tak je potřeba ukázat, že existuje nějaký kandidát na číslo R(a), které je dělitelné číslem, které není tvaru kn+1.
"Máte úhel beta." "No to nemám."
Offline
#18 16. 08. 2020 00:03
Re: Velká Fermatova věta
↑ check_drummer:
Sice jsem byl na matfyzu, ale už jsem se asi odnaučil přesnému vyjadřování :D Samozřejmě jsem myslel čísla tvaru  pro nenulové
pro nenulové  . Omlouvám se za mnoho nepřesností, příště si dám záležet, abych byl všude důsledný :D
. Omlouvám se za mnoho nepřesností, příště si dám záležet, abych byl všude důsledný :D
Offline
#19 16. 08. 2020 01:59
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
↑ liamlim_2: Spíš je důležitější druhá část mé poznámky.
"Máte úhel beta." "No to nemám."
Offline
#20 16. 08. 2020 05:03 — Editoval liamlim_2 (16. 08. 2020 05:12)
Re: Velká Fermatova věta
lcm↑ check_drummer:Skutečně? Proč nemůžeme přirozeně pro případ že takový dělitel neexistuje dodefinovat  pokud neexistuje žádný dělitel tvaru
pokud neexistuje žádný dělitel tvaru  ? Skutečně je to o tom, aby fungovalo vše jak má. Přirozeně platí
? Skutečně je to o tom, aby fungovalo vše jak má. Přirozeně platí 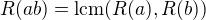 . Aby tato rovnost platila, potřebujeme
. Aby tato rovnost platila, potřebujeme  pokud neexistuje dělitel tvaru
pokud neexistuje dělitel tvaru 
Offline
#22 16. 08. 2020 09:28
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
↑ liamlim_2:
Dodefinovat to můžeme, jen je potřeba to v definici R(a) uvést, aby ta definice byla korektní.
"Máte úhel beta." "No to nemám."
Offline
#23 16. 08. 2020 09:35
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
Z čeho plyne 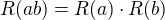 ?
?
"Máte úhel beta." "No to nemám."
Offline
#24 16. 08. 2020 09:47 — Editoval liamlim_2 (16. 08. 2020 09:48)
Re: Velká Fermatova věta
↑ check_drummer:
To vlastně neplatí, ale ono se toto tvrzení skoro nikde nevyužívá, vlastně není vůbec potřeba. Dodefinování  pokud
pokud  nemá dělitel tvaru
nemá dělitel tvaru  bylo nezbytné.
bylo nezbytné.
Já jsem ten vzorec 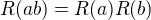 použil pouze pro odvození vztahů
použil pouze pro odvození vztahů
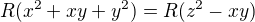
Toto odvození ale plyne přímo z definice  a vztahů (1) a (2). Pokud by totiž například
a vztahů (1) a (2). Pokud by totiž například  , pak musí existovat dělitel
, pak musí existovat dělitel  dělící pravou stranu rovnosti
dělící pravou stranu rovnosti  nebo dělitel
nebo dělitel 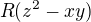 dělící levou stranu této rovnosti. V obou případech dostaneme spor, neboť libovolný dělitel
dělící levou stranu této rovnosti. V obou případech dostaneme spor, neboť libovolný dělitel  není ani
není ani  ani tvaru
ani tvaru  a současně libovolný dělitel
a současně libovolný dělitel 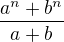 je buď
je buď  nebo tvaru
nebo tvaru  , což se vzájemně vylučuje
, což se vzájemně vylučuje
Opravdu si přeji, abych mohl původní příspěvek zeditovat a opravit veškeré chyby a překlepy
Offline
#25 16. 08. 2020 10:01
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Velká Fermatova věta
Ještě mi není jasné toto:
liamlim_2 napsal(a):
Protože
dělí
a současně
dělí
, musí
dělit též
.
"Máte úhel beta." "No to nemám."
Offline
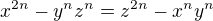 což dokážeme dosazením
což dokážeme dosazením 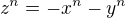
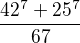 má prvočíselné dělitele 60383, 2017, 29, z nichž všechny jsou tvaru
má prvočíselné dělitele 60383, 2017, 29, z nichž všechny jsou tvaru 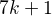 . To tvrzení pouze říká, že se nejedná o výjimku, ale že každý dělitel čísla tvaru
. To tvrzení pouze říká, že se nejedná o výjimku, ale že každý dělitel čísla tvaru 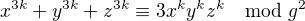
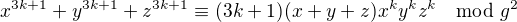
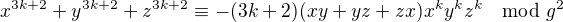

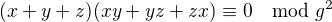 ,
,  a
a 