Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 08. 2020 21:11
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Rozvoj do Fourierovy řady
Dobrý den,
řeším Laplaceovu rovnici ale nevychází mi a proto bych Vás chtěl poprosit o překontrolování rozvoje hustoty náboje do Fouriera.
Hustota náboje 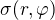 nabívá hodnot :
nabívá hodnot :

Součet řady v bodech nespojitosti: nulový protože  a
a 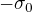 se vyruší.
se vyruší.
jedná se o sudou funkci budou tedy jen členy s cosiny:


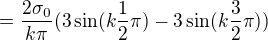
Jelikož s k=1,2,3,4,5,.. 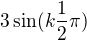 nabývá hodnot 3,0,-3,0,3,.. a
nabývá hodnot 3,0,-3,0,3,.. a 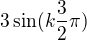 hodnot -3,0,3,0,-3,..
hodnot -3,0,3,0,-3,..
nabývá tedy jejich rozdíl 6,0,-6,0,6,.. což střídá stejně znaménka jako 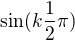 , tedy:
, tedy:
pak
Dlouho jsem rozvoje nedělal, tak budu moc vděčný když mi najdete chyby.
Díky
Petr
Offline
#3 29. 08. 2020 17:47
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Rozvoj do Fourierovy řady
↑ Brano: Díky za odpověď. Není to tedy tak, že když rozdělím integrační obor tak musím upravit i koeficient před integrálem? myslel jsem, ta pulperioda se vztahuje ke konkrétnímu integrálu části integračního oboru a jeho půl periodě a ne k celému integračnímu oboru na kterém rozvoj provádím. díky za odpověď
Offline
#4 29. 08. 2020 20:45
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Rozvoj do Fourierovy řady
Pro jistotu: Takto je to tedy správně?


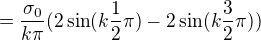

pak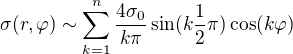
Díky
ps: ty první dva integrály jsem mohl beztrestně spojit do jednoho, že?
Offline


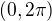 tak pred integralom mas mat
tak pred integralom mas mat 
