Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 10. 2020 00:10
Kvadratická rovnice s parametrem
Zdravím,
potřebuji pomoci s následujícím příkladem: 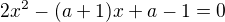 a platí
a platí 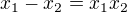 . Mám určit a.
. Mám určit a.
Šel jsem před Vietovy vzorce, nejdřív jsem rovnici vydělil dvěma
dostal jsem 3 rovnice o 3 neznámých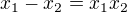
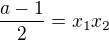
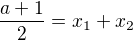
-> vyjádřil jsem si 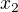 z první rovnice
z první rovnice 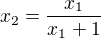
a dosadil do třetí s tím, že jsem si vyjádřil a. To mi vyšlo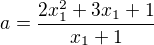 .
.
Ale když se pak snažím dosadit, tak mi to nevychází (vyjde mi že  )
)
Nějaké nápady? Řešení je 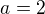
Díky
Offline
- (téma jako vyřešené označil(a) Sikys)
#2 19. 10. 2020 00:48 — Editoval Jj (19. 10. 2020 00:54)
Re: Kvadratická rovnice s parametrem
↑ Sikys:
Hezký den, možná "přímočařeji":
Řekl bych, že zadaná kvadratická rovnice má kořeny , což po jejich dosazení přímo do vztahu pro její kořeny vede ke dvěma možným rovnicím pro a:
, což po jejich dosazení přímo do vztahu pro její kořeny vede ke dvěma možným rovnicím pro a:  , která má kořen a = 2,
, která má kořen a = 2, , která nemá řešení.
, která nemá řešení.
Pokud se tedy nemýlím.
Offline
#3 19. 10. 2020 01:57 — Editoval misaH (19. 10. 2020 02:09)
- misaH
- Příspěvky: 13459
Re: Kvadratická rovnice s parametrem
No.
Moje riešenie, Jj iste prepáči - zdravím :-)
Vyšla som z troch rovníc uvedených zadávateľom.
1. Rovnice obsahujúce "a" som zrátala, dostala som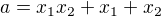
2. Vzhľadom k prvej rovnici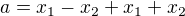
Odtiaľ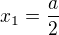
3. Dosadením do upravenej tretej rovnice a následnej doúprave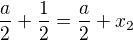
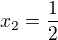
4. Dosadením do prvej rovnice zo zadania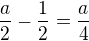
A odtiaľ už bezbolestne 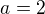
Offline
